离散数学
第七章 图
邻域、顶点的度
- 邻域
:与 相邻的点的集合,
从定义来看,有自环的点的邻域不算自身
- 关联集
:与 关联的边的集合, - 度
:与 关联的边的次数之和 - 出度、入度
注意:环对于结点度的贡献是 2,孤立顶点的度为 0
- 最大度
, ;最小度 ,
周长与围长
- 周长
:含圈的无向简单图 中, 中最长圈的长度。 - 围长
: 中最短圈的长度。
握手定理
每个图中,结点度数的总和等于边数的两倍。
有向图中,出度和与入度和相等且等于边数。
推论:在任何图中,奇数度顶点的个数是偶数。
简单图、零图、
- 简单图:无环、无平行边
- 零图:无边
辨别:平凡图:
阶零图;空图:无点
-正则图:无向简单图且各个点的度数均为
可简单图化、同构
前提:可图化(度数总和为偶数)
Havel 定理:每次删去图上度数最大的一个点,若删去后的图仍为可图化的且未出现负数度顶点,则继续,否则不可简单图化。
Erdös 定理:

同构:
Havel 定理中能选择点的时候就可以出不同构的图了吧。
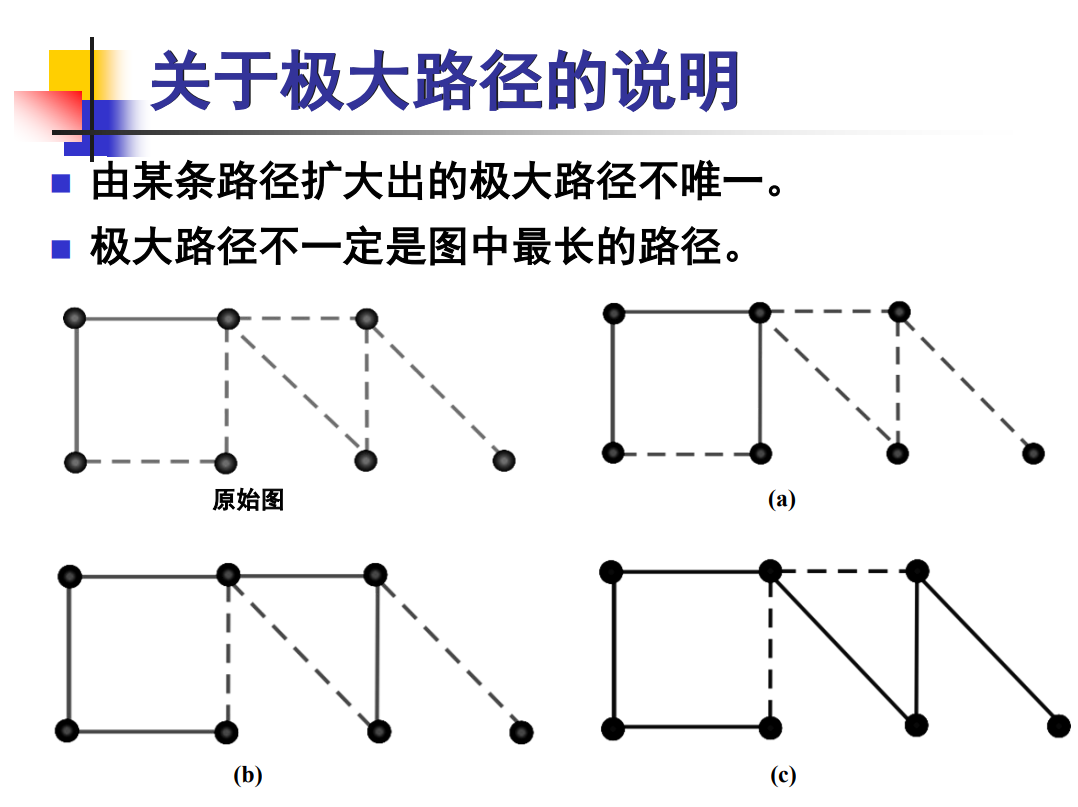
极大路径
原路径

割点、桥、点连通度、边连通度
- 割点:
- 桥:
- 点连通度
:最小的点割集中的点数,规定 ,而如果 非连通,则 。 - 边连通度
:最小的边割集中的边数,如果 非连通,则 。 - Whitney 定理:
很好理解,边割集最差情况是一个点的所有关联边,最好的情况是桥;点割集(除了割点之外)最差的就是拿掉某个边割集中的边某侧所关联的所有的点。
二部图、完全二部图
- 二部图:(定理 7.8)一个无向图
是二部图当且仅当 中无奇圈。 - 完全二部图:完全二部图
的周长是 ,围长是 。
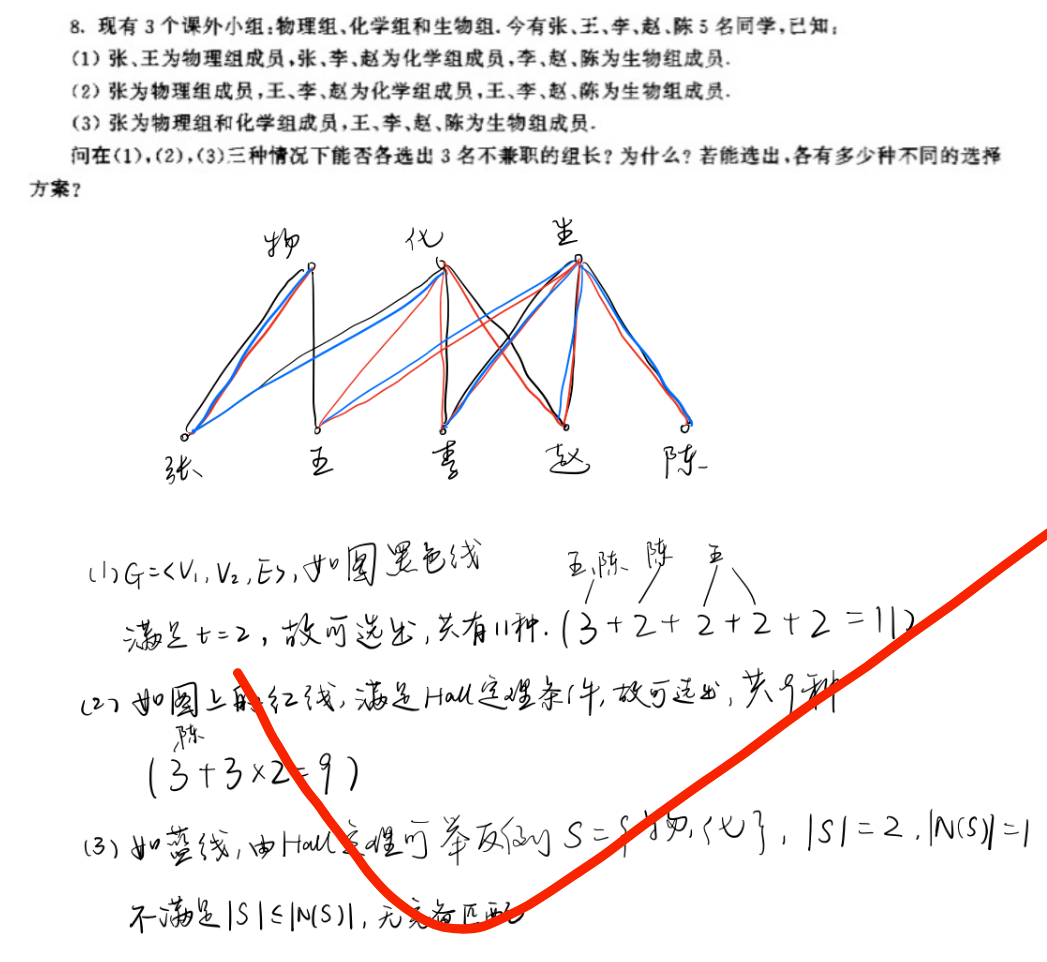
重点习题

由边数得总度数为
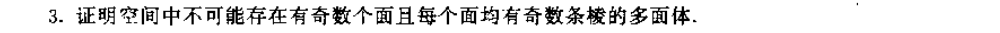
对多面体建模,设图共有
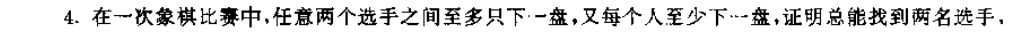

设共有
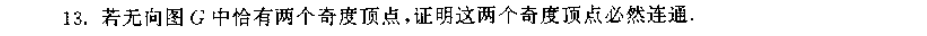
若
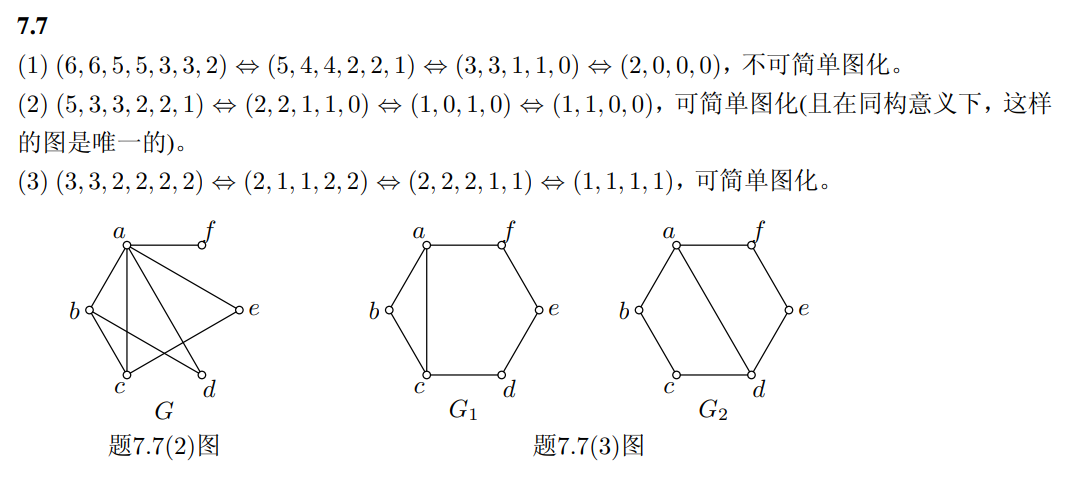


第八章 欧拉图与哈密顿图
欧拉图
- 欧拉回路:通过所有边一次的简单回路
- 欧拉路,欧拉通路:通过所有边一次的简单通路
- 欧拉图:有欧拉回路的图
- 半欧拉图:有欧拉通路,无欧拉回路的图
规定平凡图为欧拉图 辨别:平凡图:
阶零图;空图:无点 环不影响图的欧拉性
定理 1:设
是无向连通图,则 定理 2:设
是无向连通图,则 定理 3:设
是有向连通图,则
- 定理 4:设
是有向连通图,则
哈密顿图
- 哈密顿回路:经过所有顶点一次的初级回路
- 哈密顿通路:经过所有顶点一次的初级通路
初级意味着点不重
- 哈密顿图:有哈密顿回路的图
- 半哈密顿图:有哈密顿通路,无哈密顿回路的图
平凡图是哈密顿图
- 定理 6(哈密顿图性质):设无向图
是哈密顿图,则对任意 有 。 - 定理 6 推论:设无向图
是半哈密顿图,则对任意 有 。
挺好理解的,哈密顿回路就是一个大圈,拿掉一个点就可以变成哈密顿通路
定理 7:若
阶无向简单图 中,任意不相邻的顶点 和 有 ,则 中存在哈密顿通路。 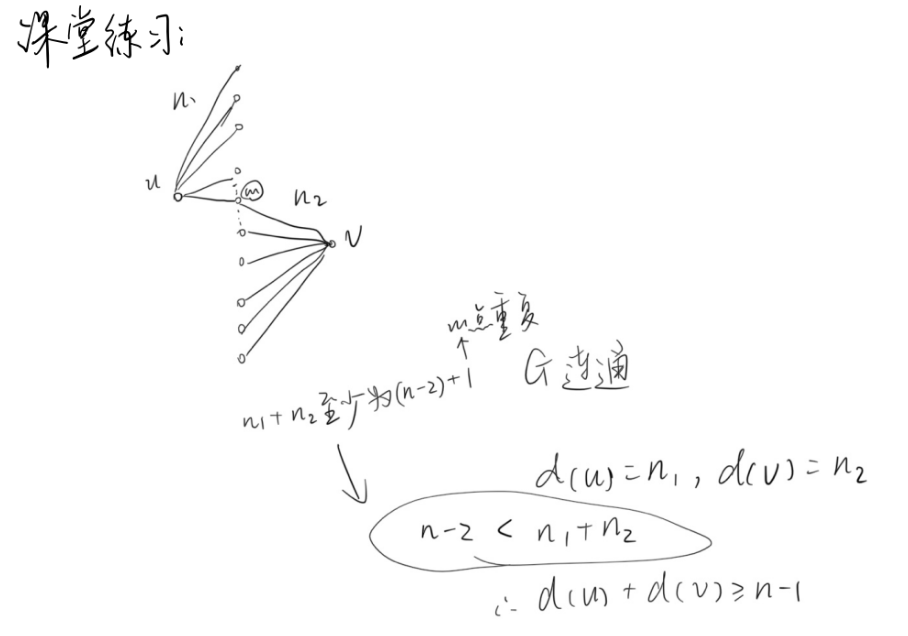
定理 7 推论(哈密顿图判定):若
阶无向简单图 中,任意不相邻的顶点 和 有 ,则 是哈密顿图。
完全图
- 定理 11:完全图
中含 条边不重的哈密顿回路,且这些回路中含 中的全部边。 - 定理 11 推论:完全图
中含 条边不重的哈密顿回路,删除这些边之后得到的是一个匹配。
重点习题
欧拉图是若干个边不交的圈的并,至少拿掉 2 条边才能破坏其连通性。
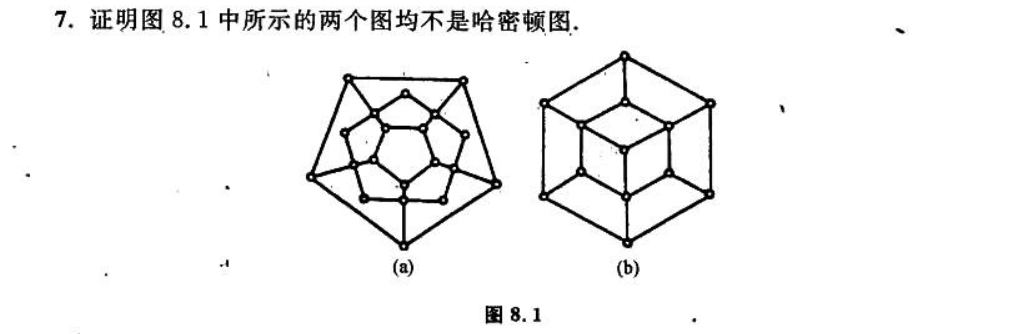
用这个定理定理 6(哈密顿图性质):设无向图



构造哈密顿回路,保证每个点都能有边。




第九章 树
树
定理 1(六个等价定义):
生成树
- 生成子图:包含所有顶点的子图
导出子图:选边,再往点集加关联的点
- 生成树
: 是 的生成子图且是树。 - 定理 3(存在定理):无向图
具有生成树当且仅当 是连通的。 - 生成树的求法:
破圈法:若图中无圈,则图本身就是生成树。否则删去圈上的任一条边,这不破坏连通性,重复进行直到无圈为止,剩下的图是一棵生成树。
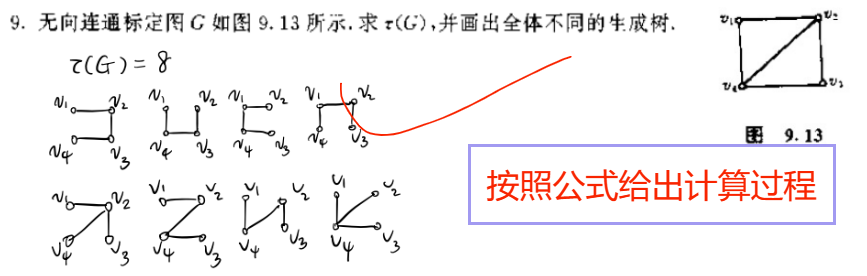
定理 6(求生成树的个数
): 定理 3:记
是 中任意 列组成的方阵,则 。 - 忽略环,求关联矩阵
- 任选参考点,求基本关联矩阵
- 求所有
阶子方阵,计算行列式,行列式非 的是生成树
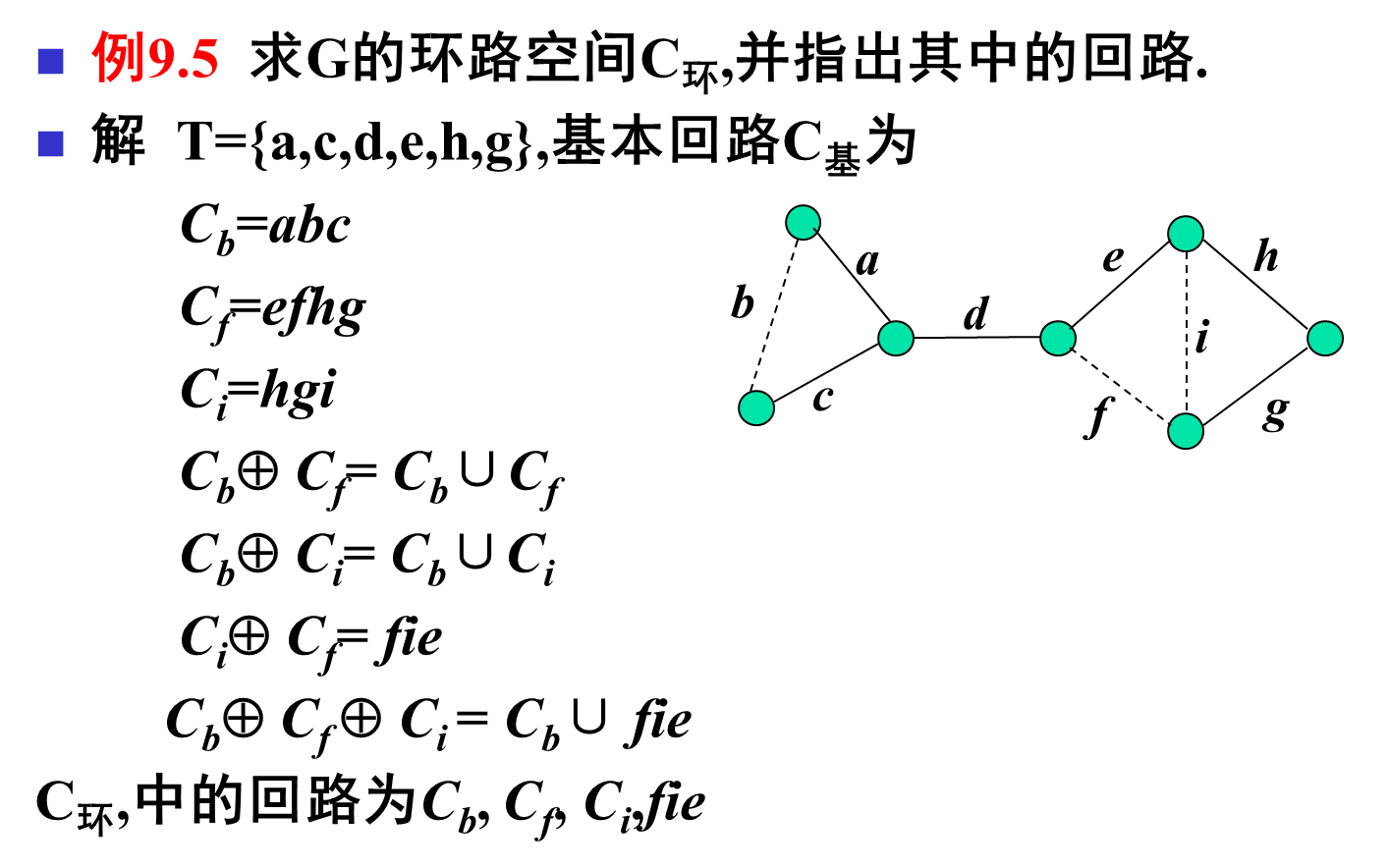
基本回路系统、环路空间
- 通过弦确定基本回路,给出基本回路系统
- 利用基本回路系统中的元素进行环合运算(参与运算的元素从
个开始到所有元素一起参与)
- 维数:
基本割集系统、断集空间
割集是断集,断集不一定是割集(可满足连通分支数目增加,但不一定满足极小性)
- 通过树枝确定割集,给出基本割集系统
- 利用基本割集系统中的元素进行对称差运算
- 维数:

根树
- 根树是有向树,其为平凡树或只有一个顶点入度为
而其他顶点的入度均为 。 - 顶点
的层数 :从树根到 路径长度 - 树高
:顶点的最大层数
叉树: - 正则
叉树:每个分支点恰好有 个儿子 - 完全正则
叉树:树叶的层数均为树高的 叉正则树 - 定理 14.13:设正则
叉树 有 个分支点和 个树叶,则 。 - 证明:握手定理,有向图的出度和和入度和相等且等于边数。
重点习题





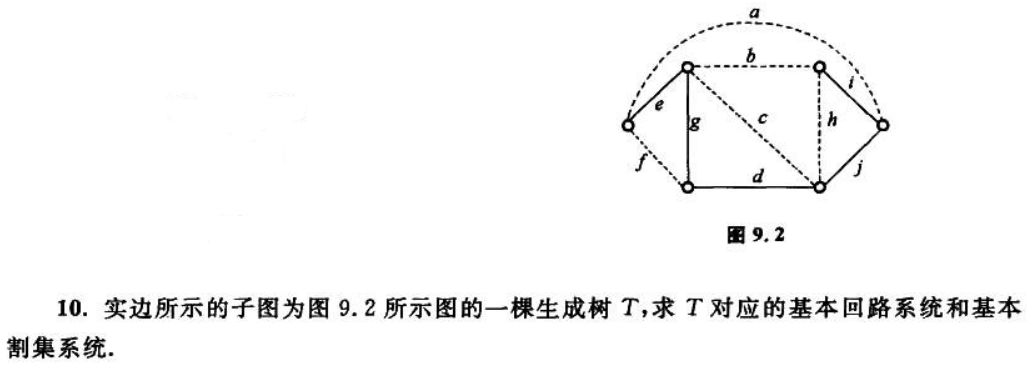


第十章 图的矩阵表示
关联矩阵
行为点,列为边。
有向图:
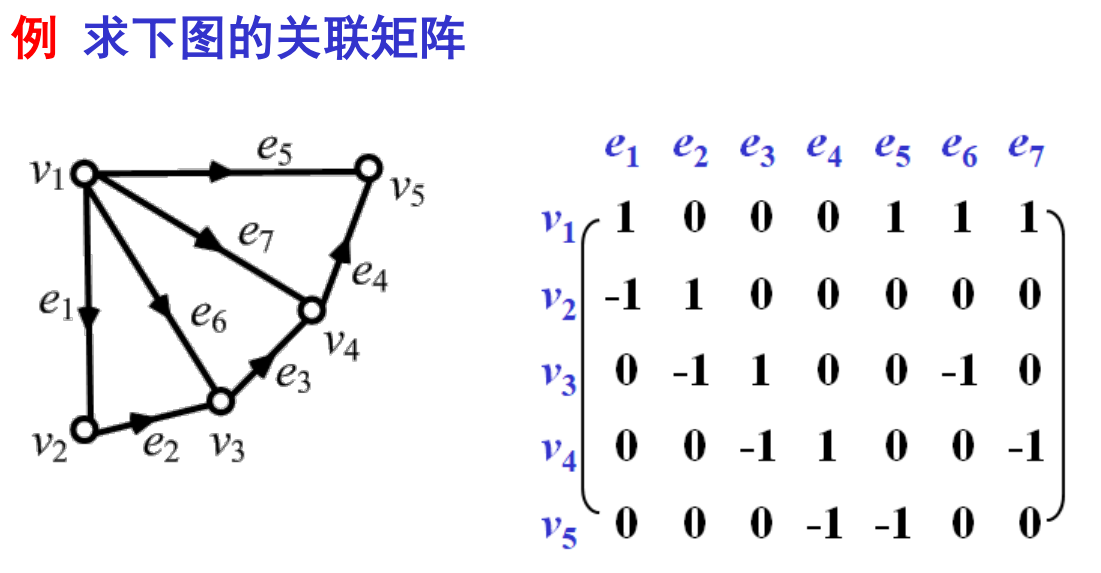
无向图:
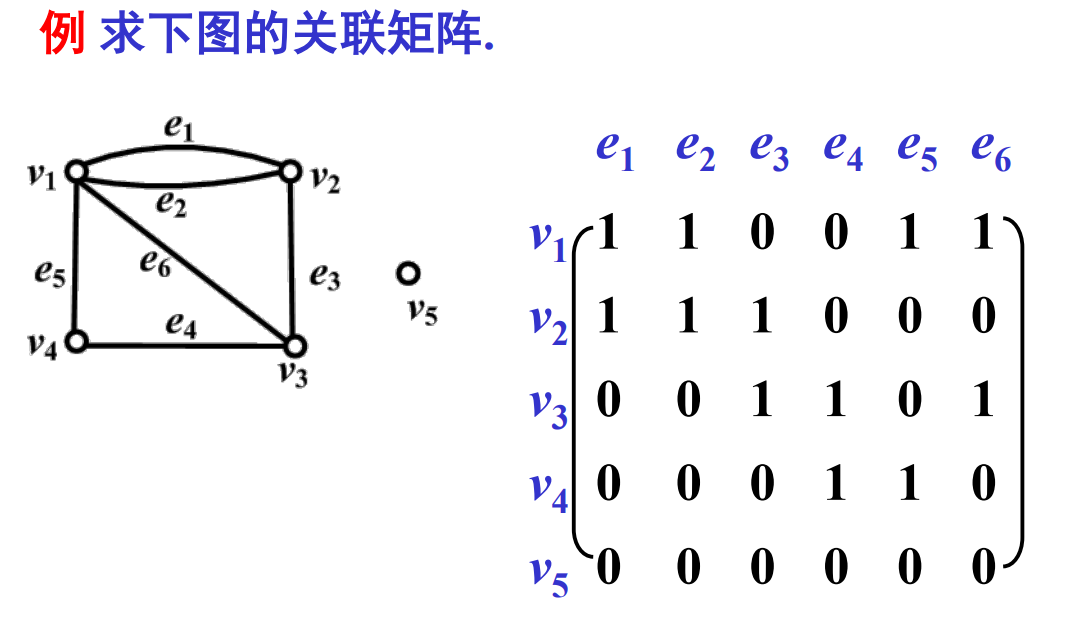
性质:
- 平行边对应的列相同
- 不能表示自环
- 无向图关联矩阵中,每行所有
对应的边构成断集
基本关联矩阵:选取一个参考点,从关联矩阵
中删除参考点对应的行,记作 。
邻接矩阵、相邻矩阵
可以表示环,
有向图邻接矩阵:
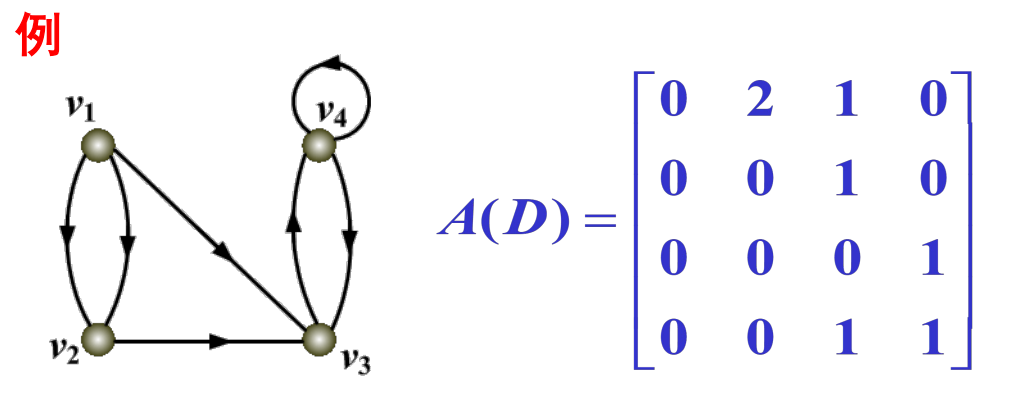
- 每行和为出度,每列和为入度,主对角元表示环
邻接矩阵求通路数:
即 经过 到 的边数 


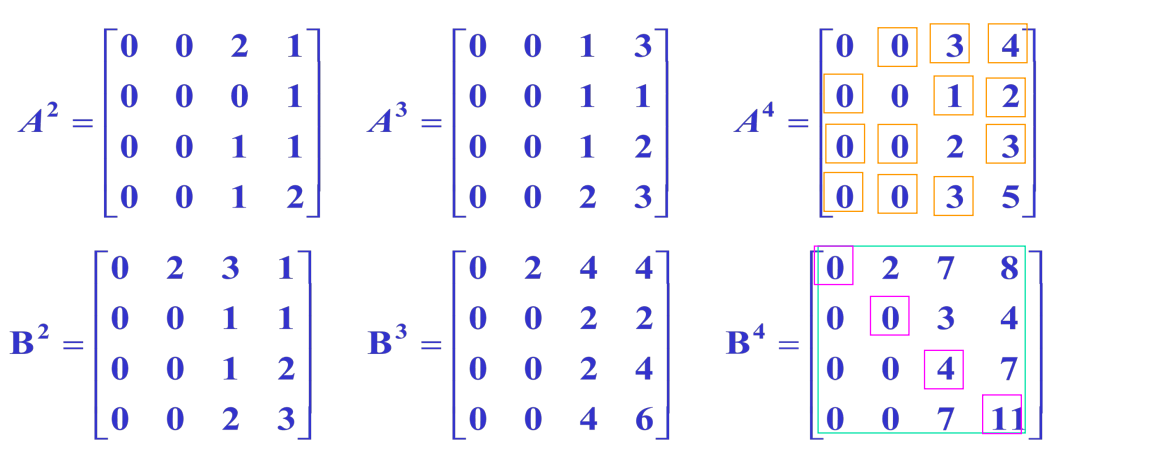
- 对每个非
元和主对角元置 ,即可得到可达矩阵。
- 对每个非
无向图相邻矩阵:是对称矩阵。
- 使用相邻矩阵求通路数、连通矩阵,和邻接矩阵相似。
重点习题
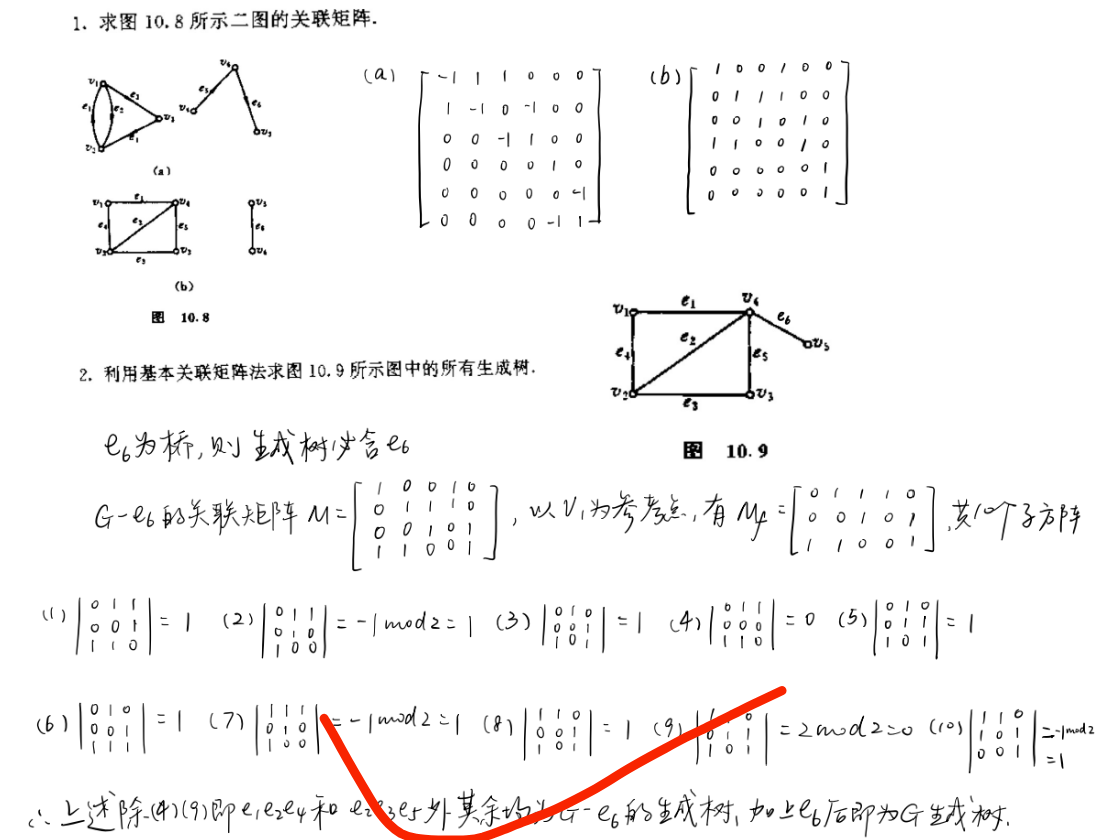

使用基本关联矩阵法。

第十一章 平面图
平面图
- 可平面图/平面图:可以画在平面上,使得边与边不在非顶点处相交的图
- 平面嵌入(平面表示):画在平面上使得边与边不在非顶点处相交的图
可平面图主要表明图具有平面性质,平面嵌入是平面图的一种表示形式,平面图的平面嵌入不唯一
性质
定理 2:所有面的次数和为边数的两倍。(其实就是握手定理)
定理 8、定理 9:

定理10:

定理11:

定理12:简单平面图
, 。
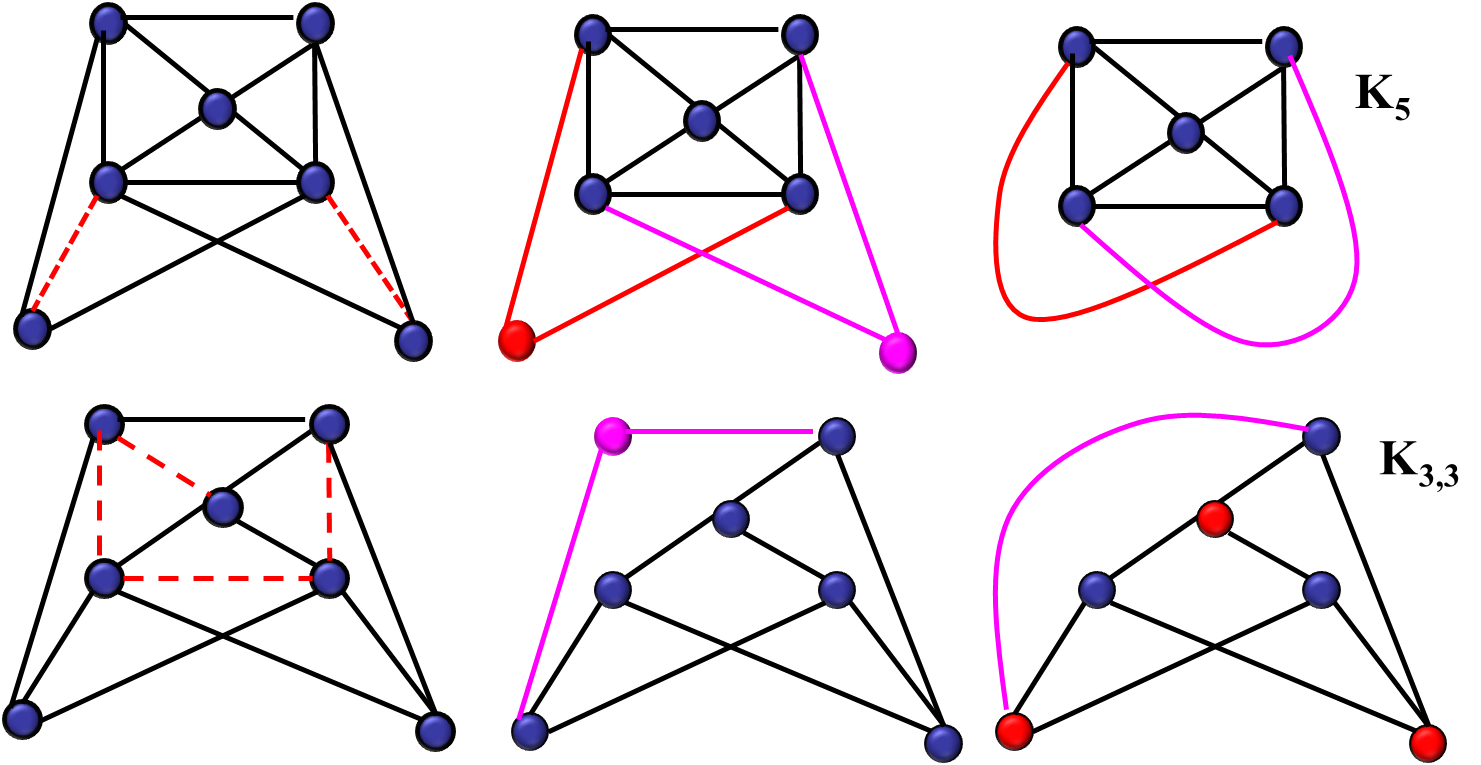
Kuratowski 定理(平面图判定定理)
例题:
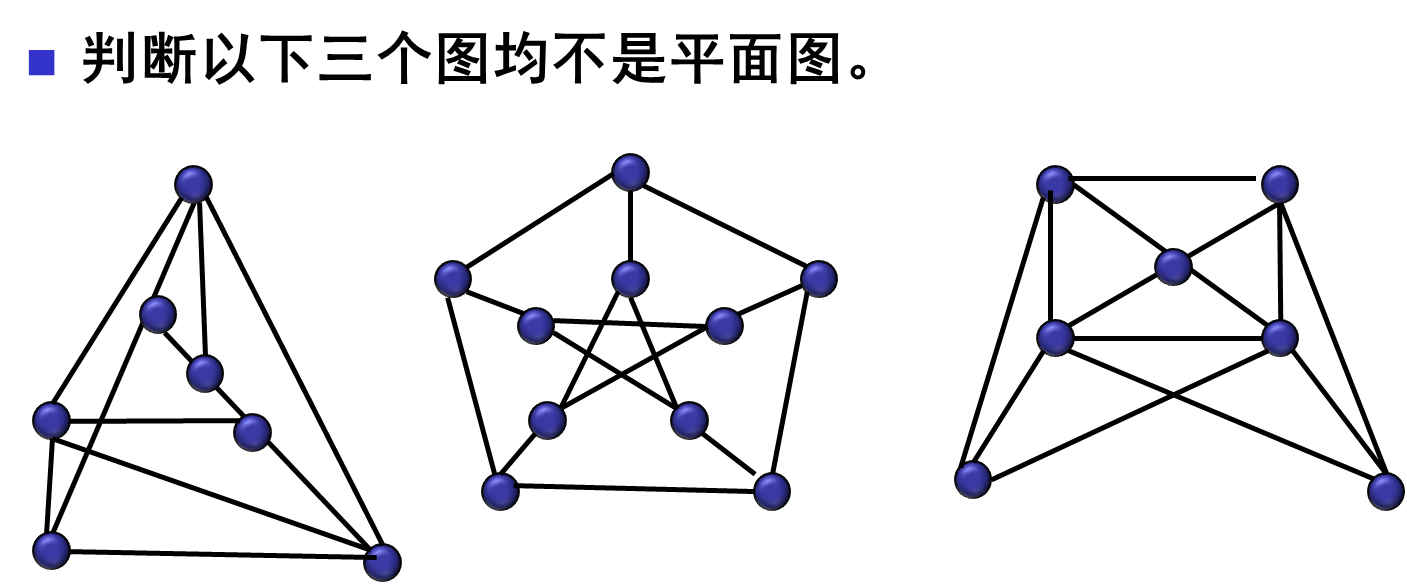
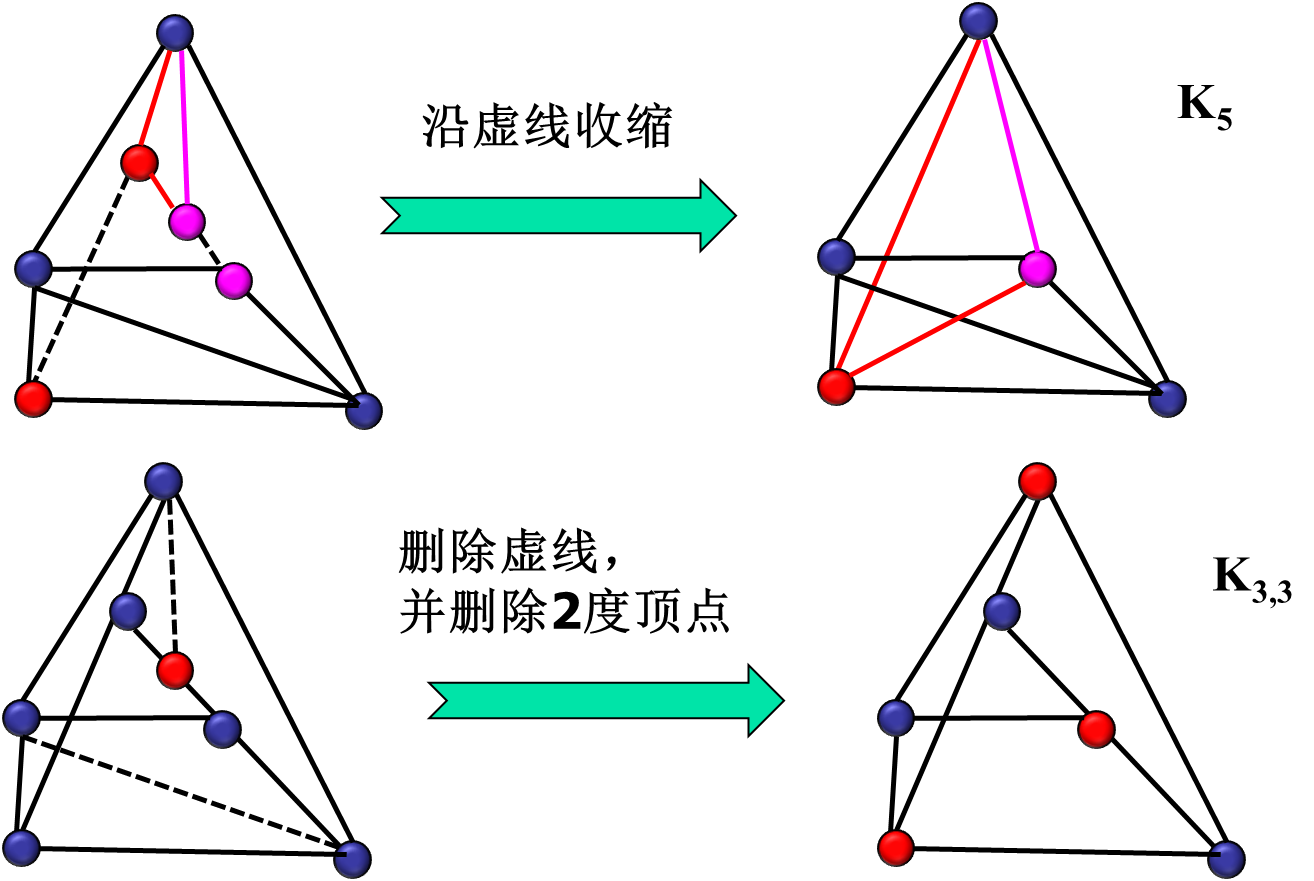
这里为什么可以删除边呢?因为定理要求的是没有和
或 同胚的子图。 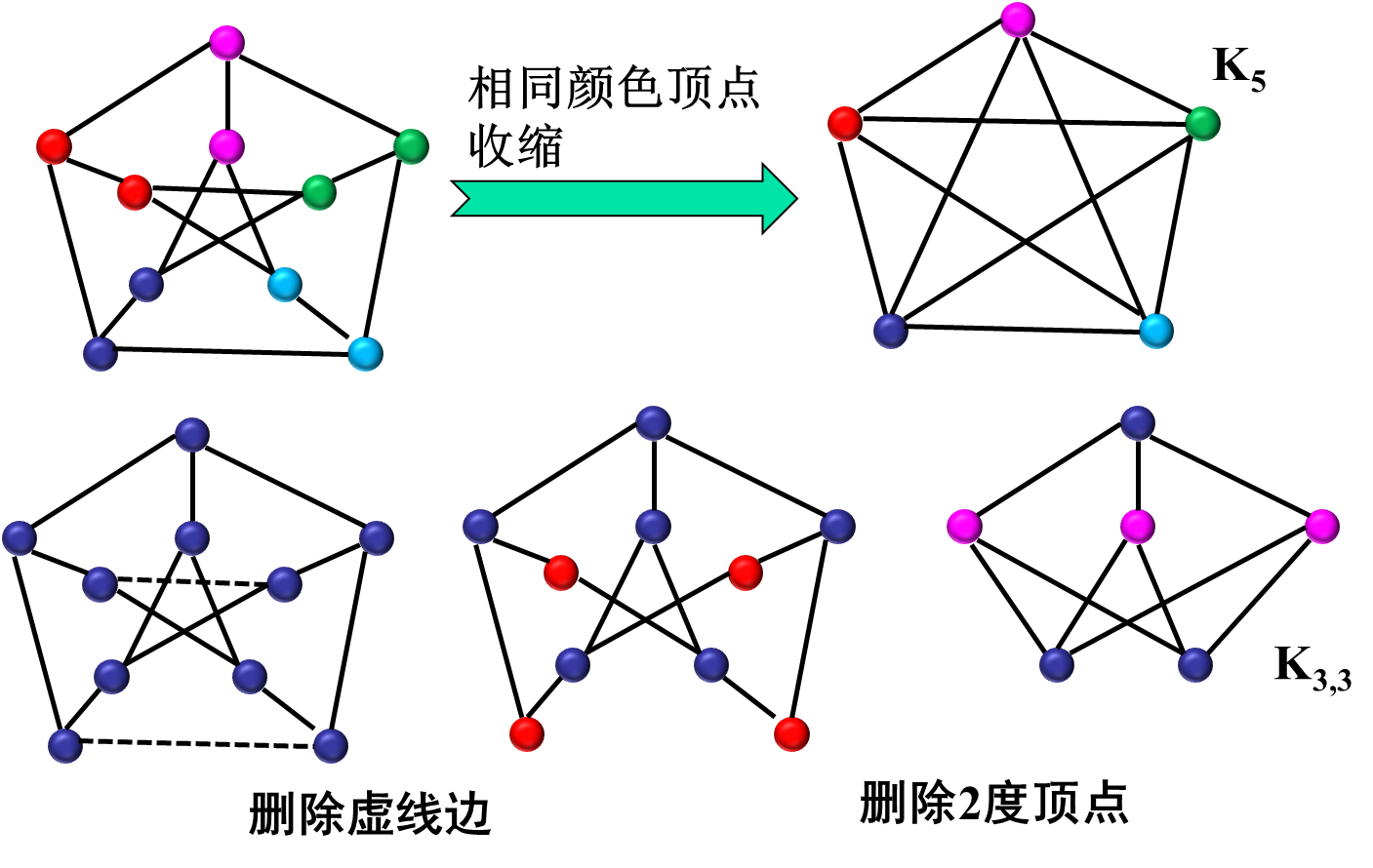
极大平面图
- 极大平面图:是平面图,但在任意两个不相邻顶点之间加边就是非平面图。
- 性质:
一定连通,否则不极大
不含有割点和桥。如果含有割点,则一定可以加边。
定理 4:


不能同时把
和 在不经过该平面内的情况下都连起来 
欧拉公式
- 欧拉公式:
- 推广:
对偶图、自对偶图
- 在
的每个面内取一个点作为顶点 - 如果两个面有公共边,则将两个面取的顶点过公共边连边。如果是悬挂边,那就是自环。
性质:
- 无论原图如何,对偶图
是连通的。
很好理解,因为一定有一个外部面的点
- 定理 15:
- 定理 16 同欧拉公式推广。
- 无论原图如何,对偶图
自对偶图:
轮图
:阶数 ,外圈 时,轮图 是自对偶图
重点习题
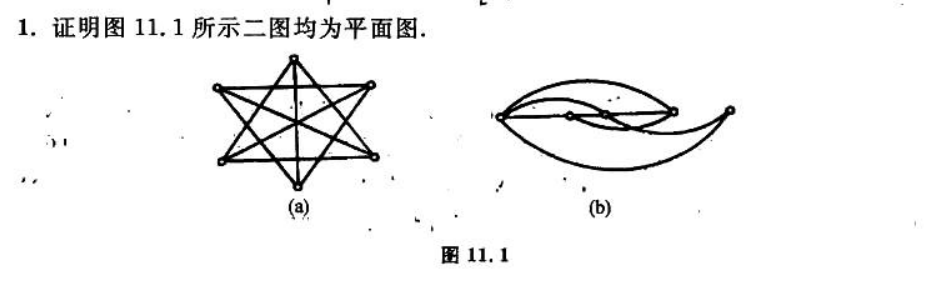
只需构造其平面嵌入。
证明非平面图时需要用Kuratowski 定理(平面图判定定理) 。


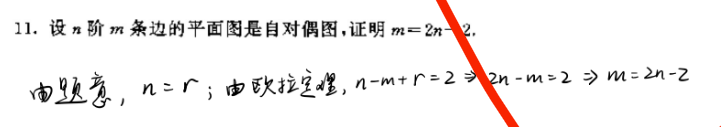

平面图有
(
(
第十二章 图的着色
色数
点色数
- 特殊的点色数
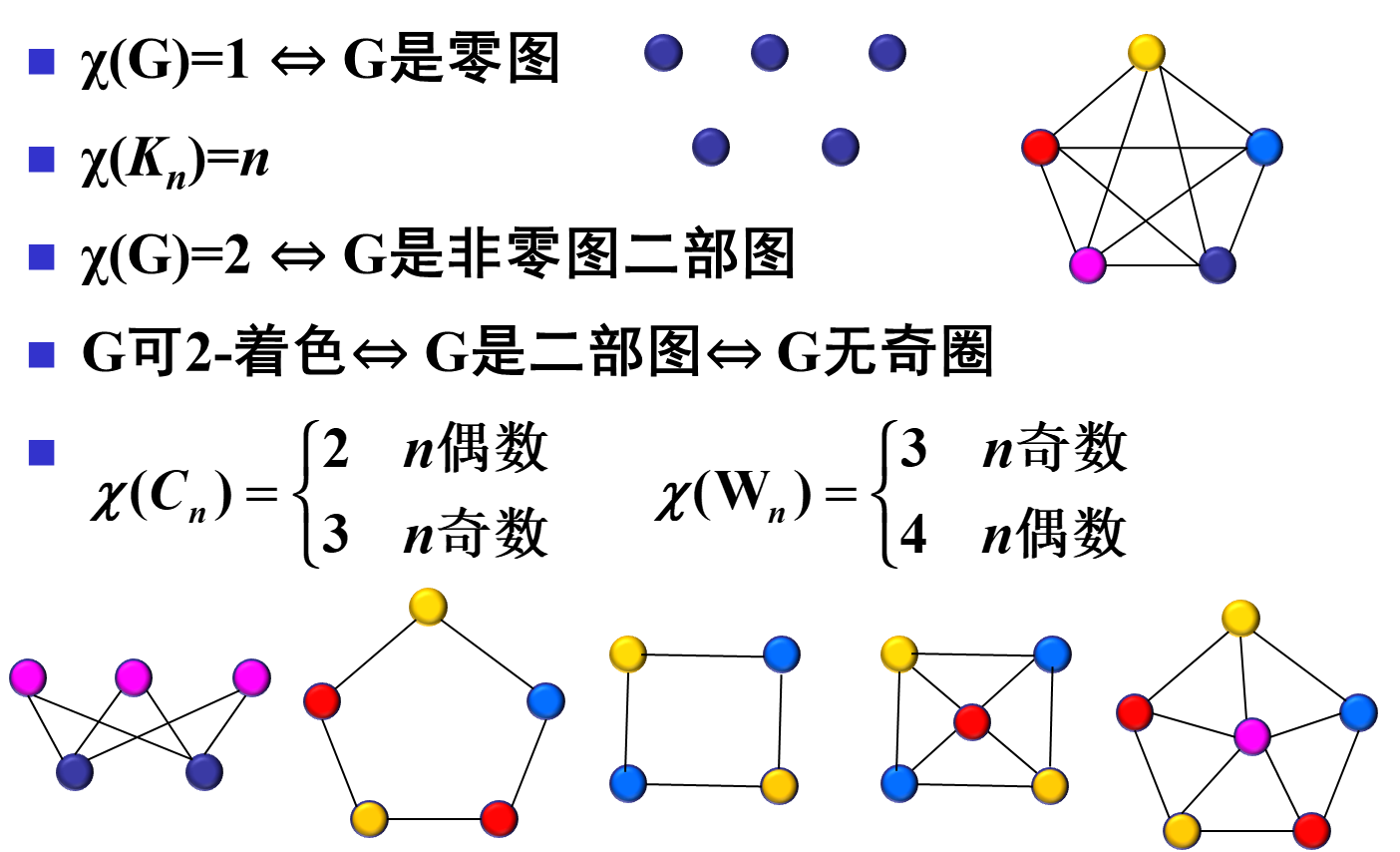
- 定理 5:
很好理解,这里的
就是 的那个点。 - 定理 6(Brooks 定理):若连通图
不是完全图 ,也不是奇圈,则 。
相邻点中有两个点着同色,只要这两点不相邻就行,不是完全图保证了这一点。而如果是奇圈,
,但 。 边色数
- 特殊的边色数
- 二部图
, - 完全图
: 时,
- 二部图
- 定理 17(Vizing 定理):
- 特殊的边色数
面色数
- 定理 13、14:研究平面图面着色⇔研究平面图点着色
五色定理
定理 15:任何平面图都可
-着色。 
定理 16:任何平面图都可
-着色。 


色数多项式
- 递推公式:
加边约束了着色条件,所以加上收缩边的色数;减边放宽了着色条件,所以减去收缩边的色数。
特殊的色数多项式
- 零图:
各个点相互独立
- 完全图:
每加入一个点,就用掉一种颜色
- 树:
树根有
种着色方式,对于每个后代只需要选择和父节点不同的颜色就可以,所以除了树根之外的 个顶点各有 种着色方式。 - 圈:
- 零图:
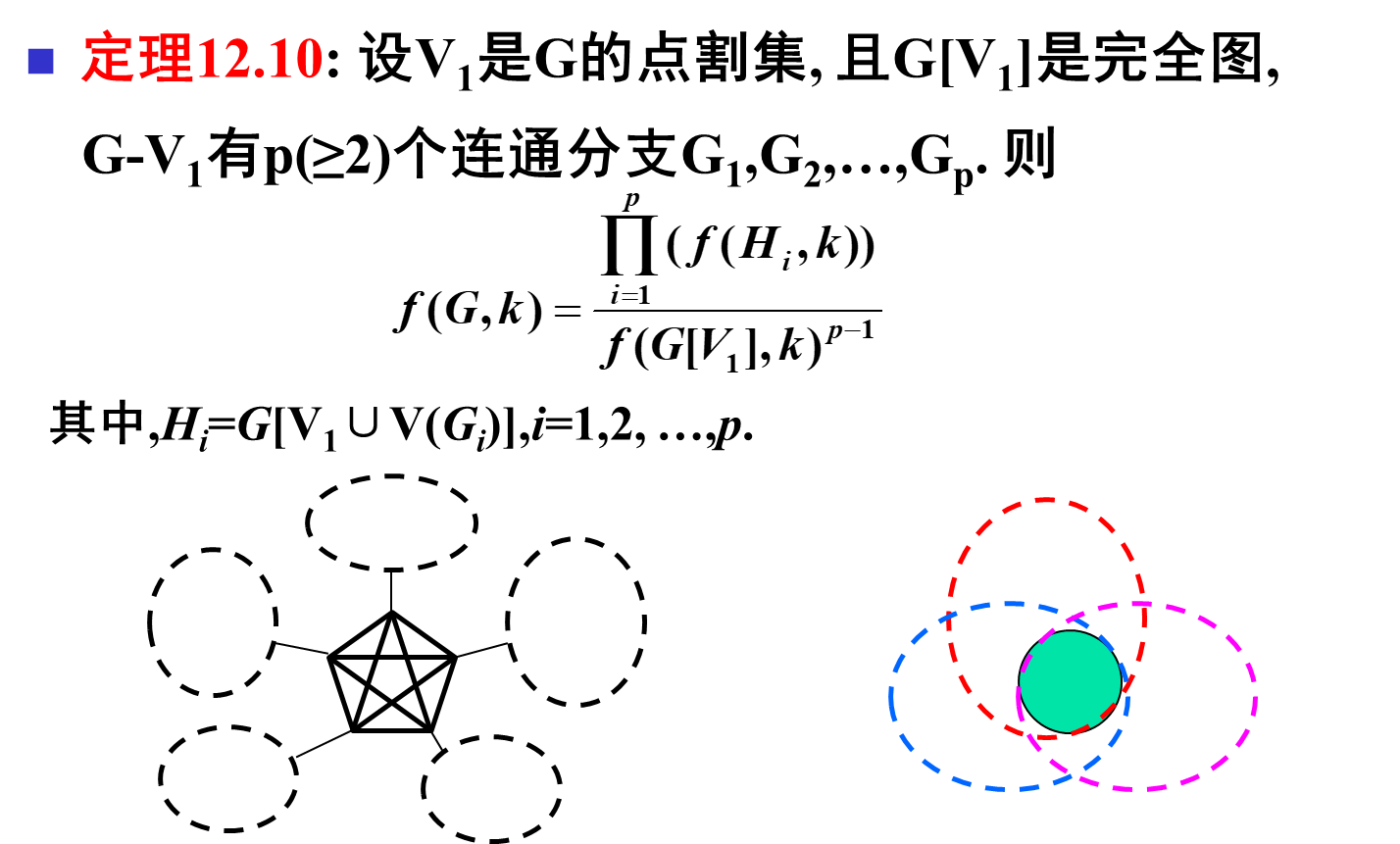
应用



- 同色边构成“边独立集”, 或“匹配”

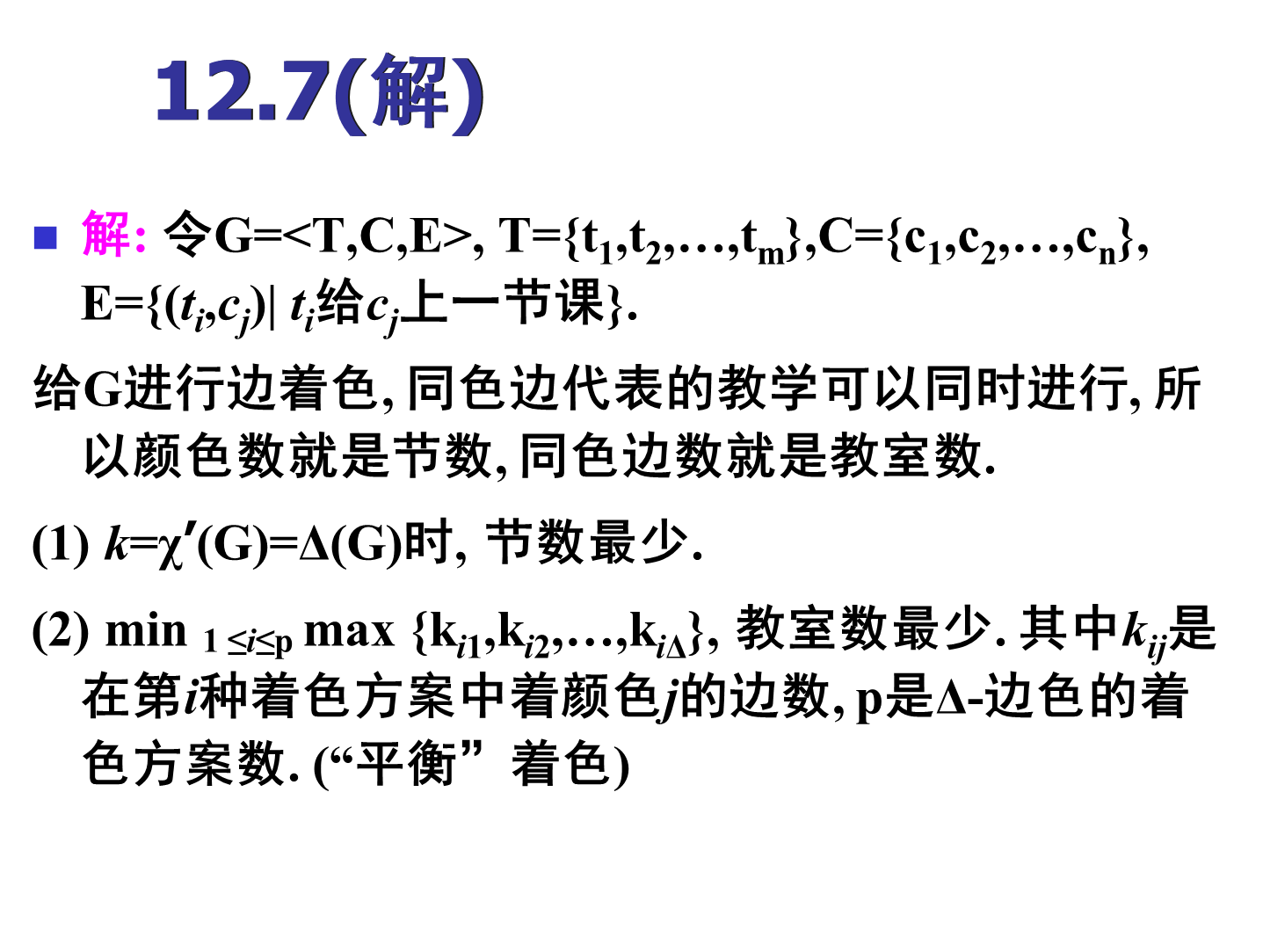

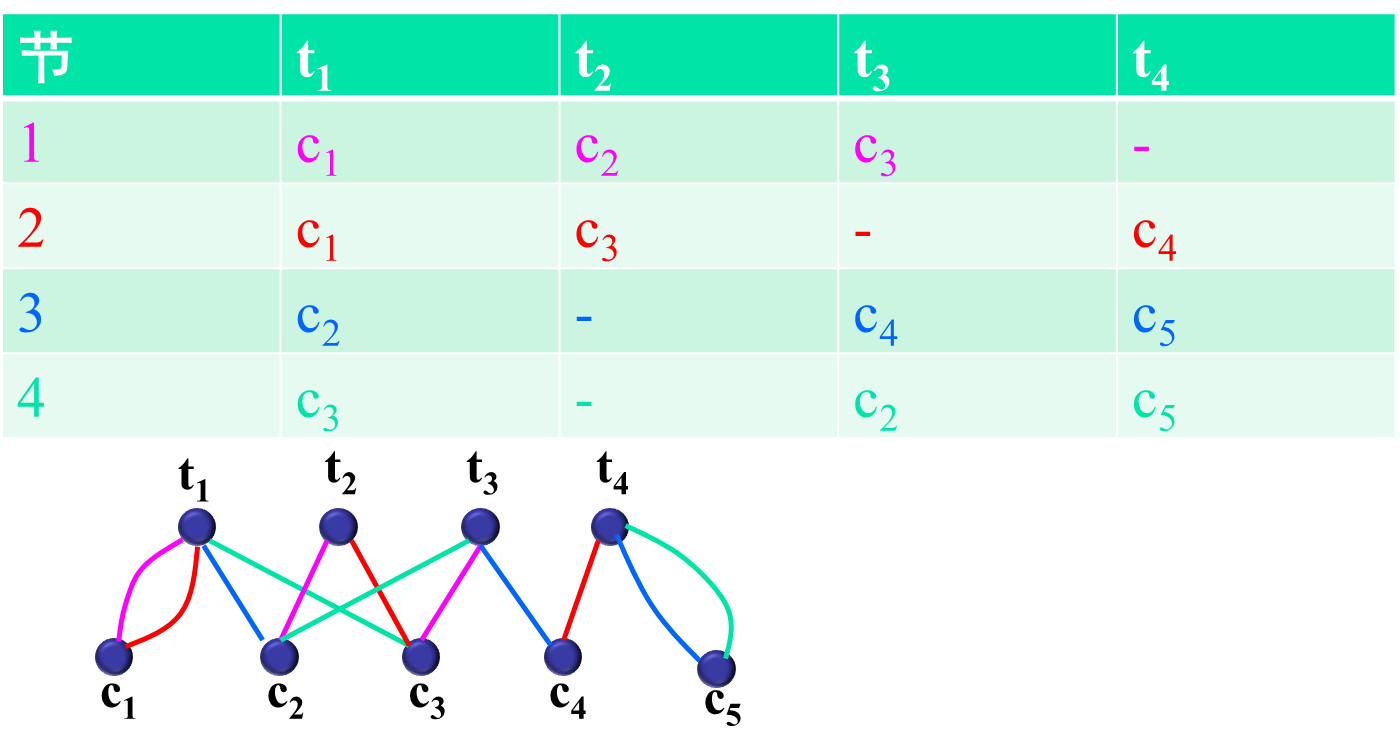
重点习题
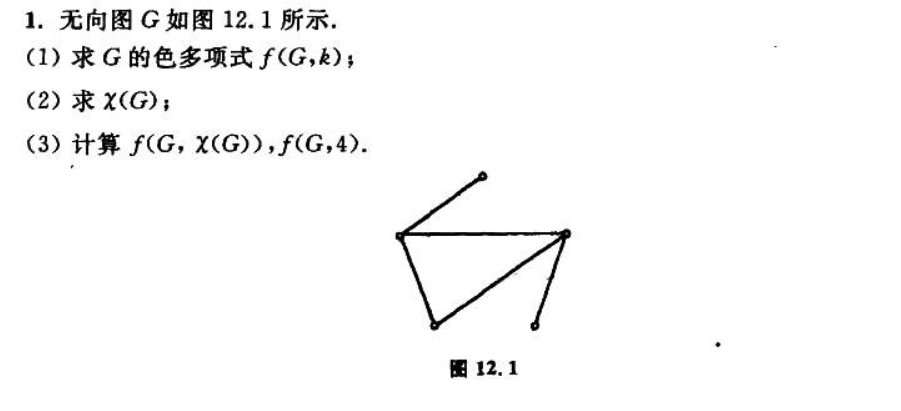
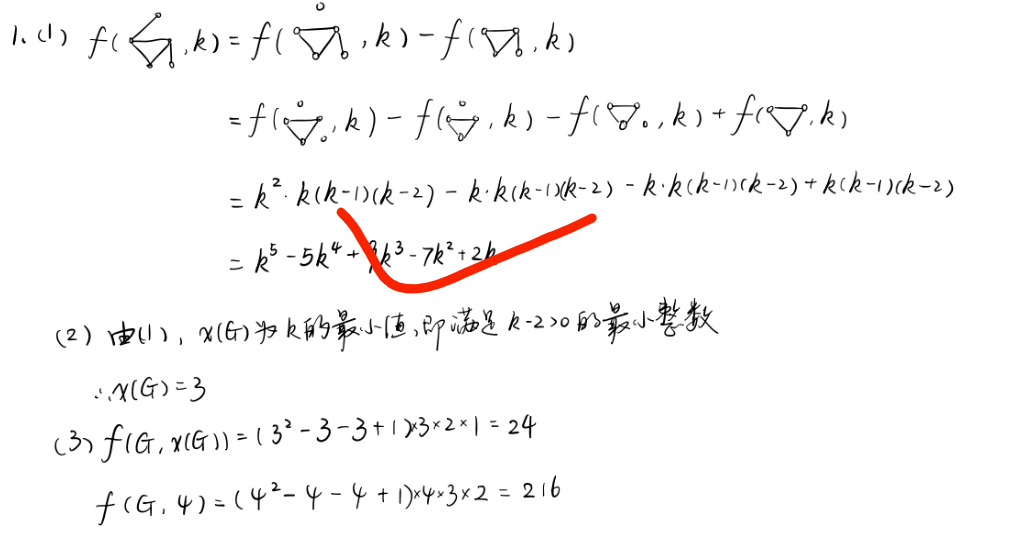





第十三章 支配集、覆盖集、独立集与匹配集
支配集
- 支配集:是点集
的子集,满足任何在 中的点能和 中的某点相邻。 - 极小支配集:真子集都不是支配集的支配集。
- 最小支配集:
最小的支配集 - 支配数
: , 是最小支配集 - 定理 1:无向图
无孤立点,如果 是极小支配集,则在 中存在 也是极小支配集。
点覆盖
- 点覆盖:
- 极小点覆盖:真子集都不是点覆盖的点覆盖。
- 最小点覆盖:
最小的点覆盖 - 点覆盖数
: , 是最小点覆盖
边覆盖
- 边覆盖:
- 极小边覆盖:真子集都不是边覆盖的边覆盖。
- 最小边覆盖:
最小的边覆盖 - 点覆盖数
: , 是最小边覆盖
独立集
- 独立集:独立集中任意两点之间没有边
- 极大独立集:真母集都不是独立集的独立集
- 最大独立集:
最大的独立集 - 独立数
: 是最大独立集 - 定理 2:无向图
无孤立点,则图中的极大独立集是极小支配集。
逆命题不成立
定理 3:无向图
无孤立点, 。 定理 3 推论:
, 
匹配(边独立集)
- 匹配数
: , 是最大匹配

最大匹配:
- 定理 9(Berge 定理):
- 定理 9(Berge 定理):
完美匹配:没有非饱和点的匹配。
- 定理 10(Tutte 定理):
, 是奇数阶连通分支数
- 定理 10(Tutte 定理):
完备匹配:二部图小的那一部分均为饱和点的匹配。
- 定理 11(Hall 条件):
,相异性条件 - 定理 12(t 条件):设
是二部图,若 中每个顶点至少关联 条边,而 中每个顶点至多关联 条边,则 中存在完备匹配。
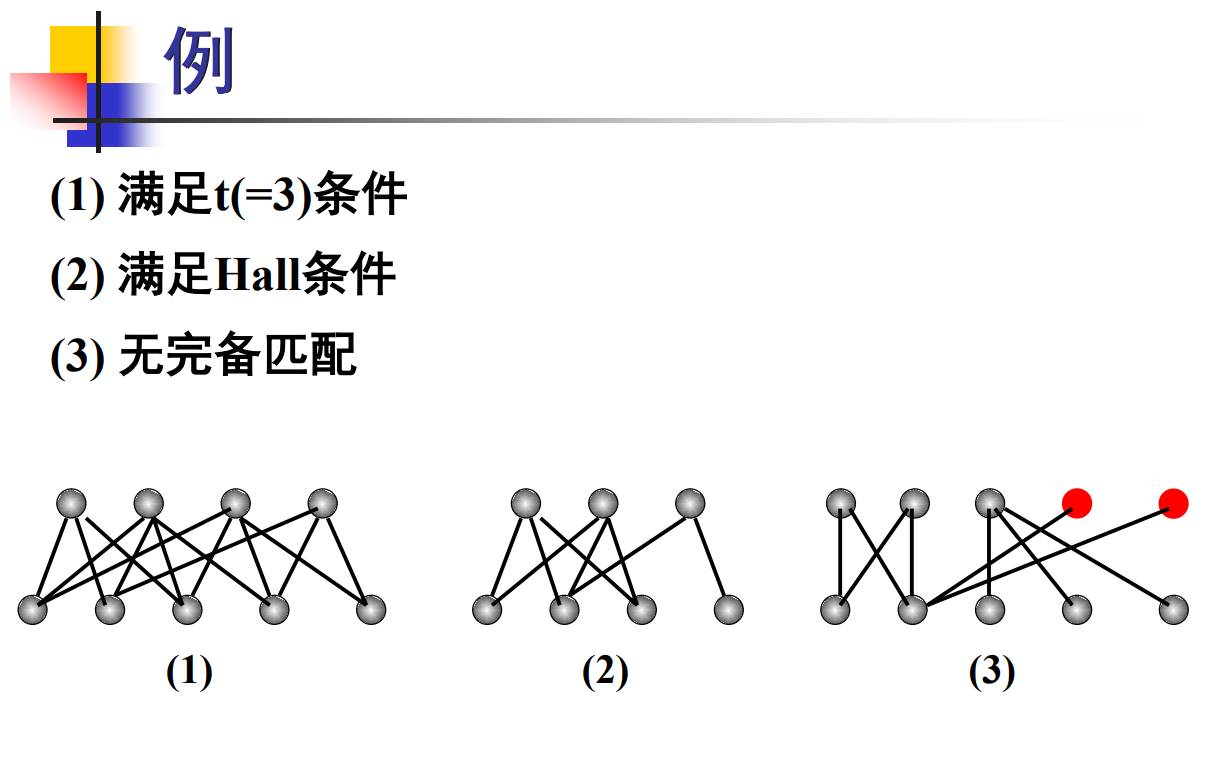
- 定理 11(Hall 条件):
团
- 团:
是完全子图 - 极大团:
是团,其真母集都不是 - 最大团:
最大的团 - 团数:
, 是最大团
运算律(不知道有没有用)

重点习题