关系数据库
关系模型
关系模型由关系数据结构、关系操作集合和关系完整性约束三部分组成。每个关系是一个二维表,每行对应一个元组,每列对应一个域,对于不同关系的相同域,需要起别名以区分,即属性。
能唯一标识元组的属性组(且其子集不能)被称为候选码,选定其中一个作为主码。一个关系的主码作为另一个关系的属性时,如果该属性在另一个关系中不是主码, 那它就是外码。
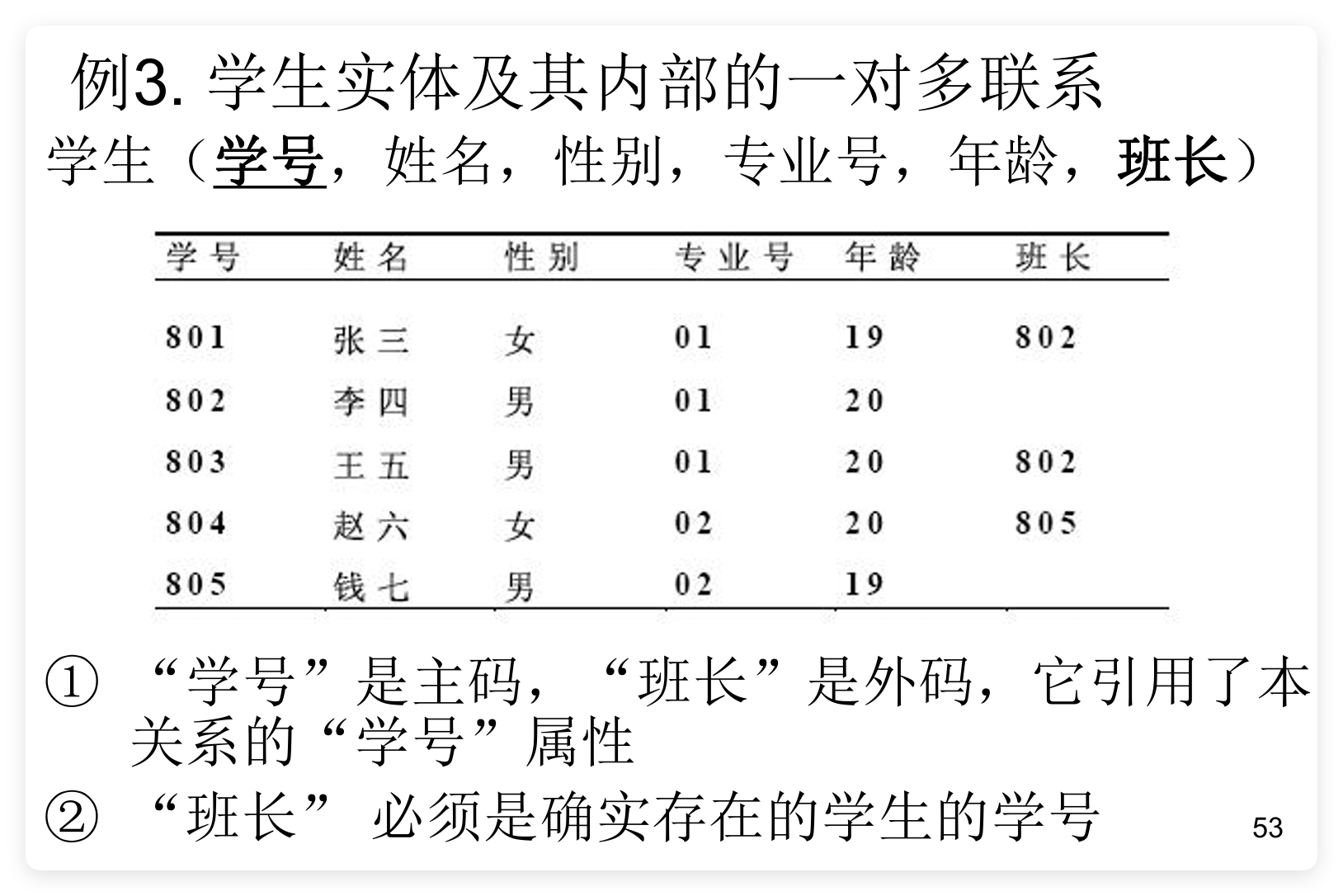

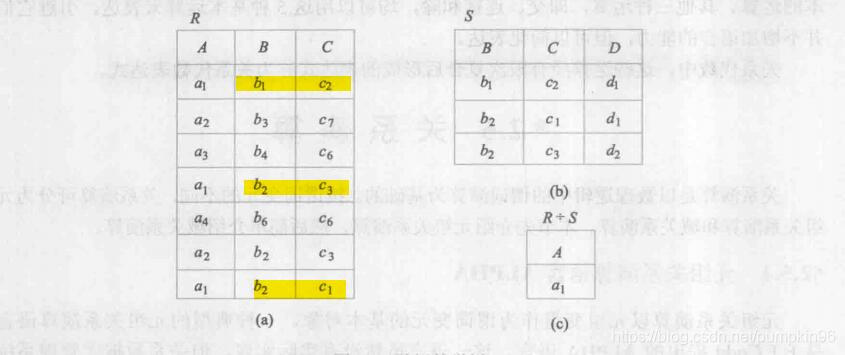
最极端的情况,当关系模式的所有属性都为候选码的时候,就称这个关系为“全码”。
完整性规则
关系模型中的三类完整性约束:实体完整性、参照完整性和用户定义的完整性。
- 实体完整性规则:主属性不能为空。
- 参照完整性规则:外码要么为空,要么为其对应的主码值。
- 用户定义的完整性:反映某一具体应用所涉及的数据必须满足的语义要求。
关系代数
运算符
集合运算符
运算符 含义 并 差 交 笛卡尔积 专门的关系运算符
运算符 含义 选择 投影 连接 除
集合运算
对于集合运算而言,除了笛卡尔积外,均要求两个关系的属性各取自同一个域。
差(
笛卡尔积的做法是把两个关系的元组各自”拼接“,元组的前
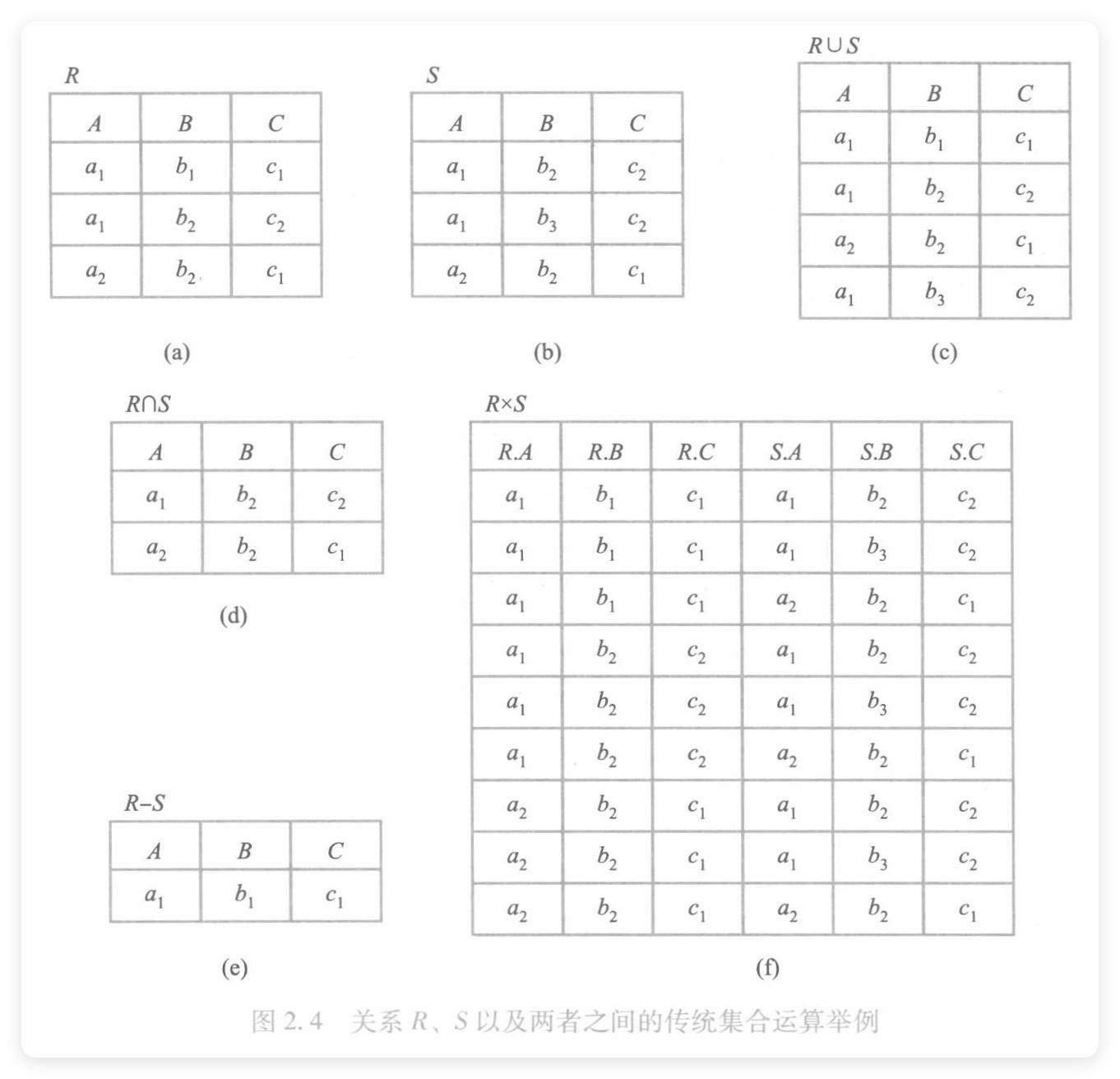
关系运算
设关系模式为
如果有一属性组

选择
:在关系 中选择满足给定条件的诸元组,是从行的角度进行的运算。 投影
:从 中选择出若干属性列组成新的关系,是从列的角度进行运算,为避免重复行可能还删掉了一些元组。 连接
:从两个关系的笛卡尔积中选取属性间满足一定条件的元组。 - 等值连接
:从笛卡尔积中选取 , 属性值相等的那些元组进行比较、连接,保留两个属性列。 - 自然连接
:特殊的等值连接,两个关系中具有相同的属性组,进行等值连接后去掉重复的属性列。 - 外连接:保留被舍弃的元组,在其他属性上填空值(NULL)。如果保留左边关系的就是左外连接,右外连接同理。
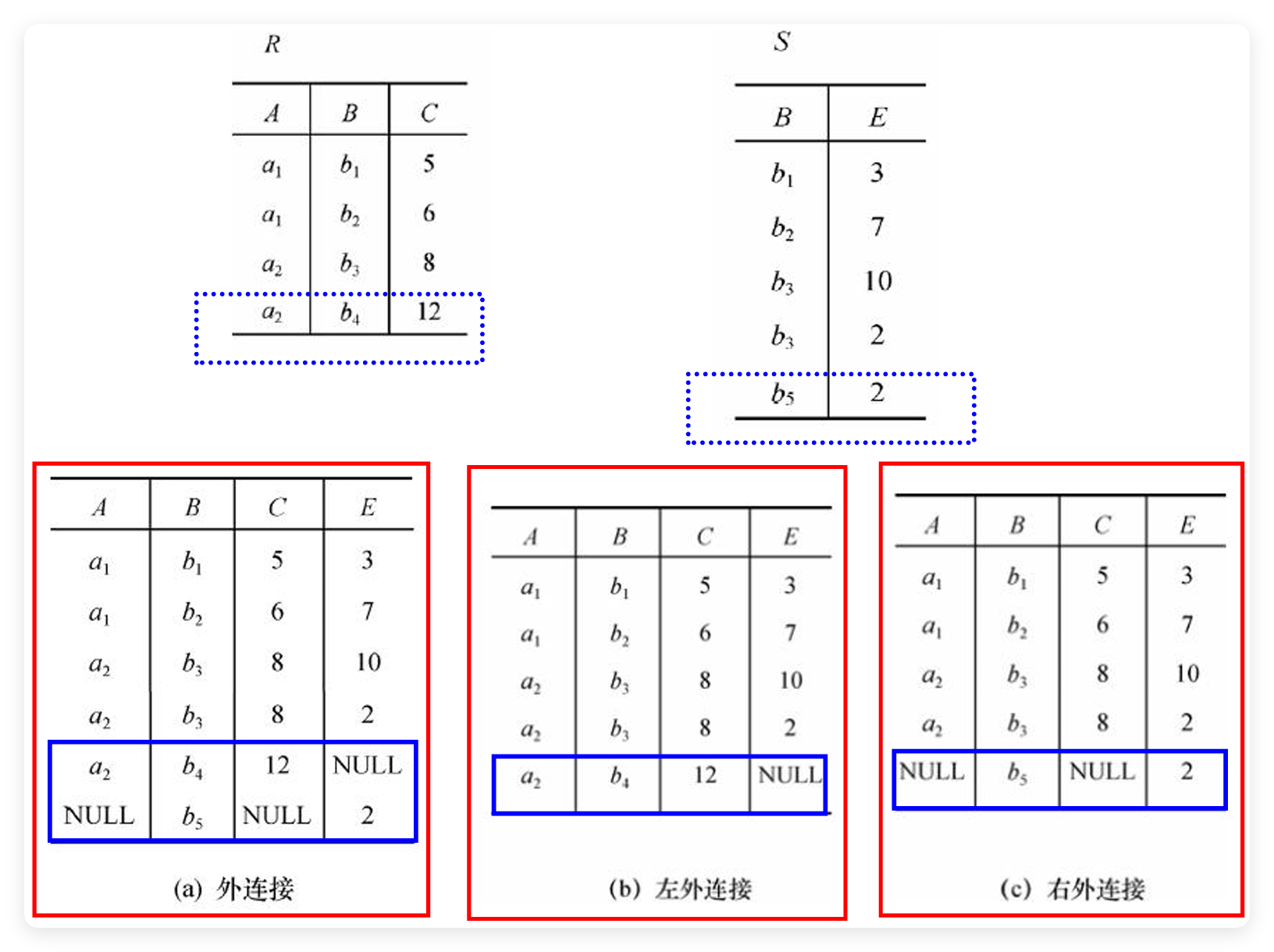
- 等值连接
除运算:
得到的属性列是 包含而 不包含的,对 剩下的属性列取象集,只保留在 中有出现的。