实验 2:深度学习基础
一、实验内容
Pytorch 基础练习
首先对 tensor 的各种形状进行摸索。在原来代码的基础上,添加一行 print(x.shape) 以打印张量的大小。
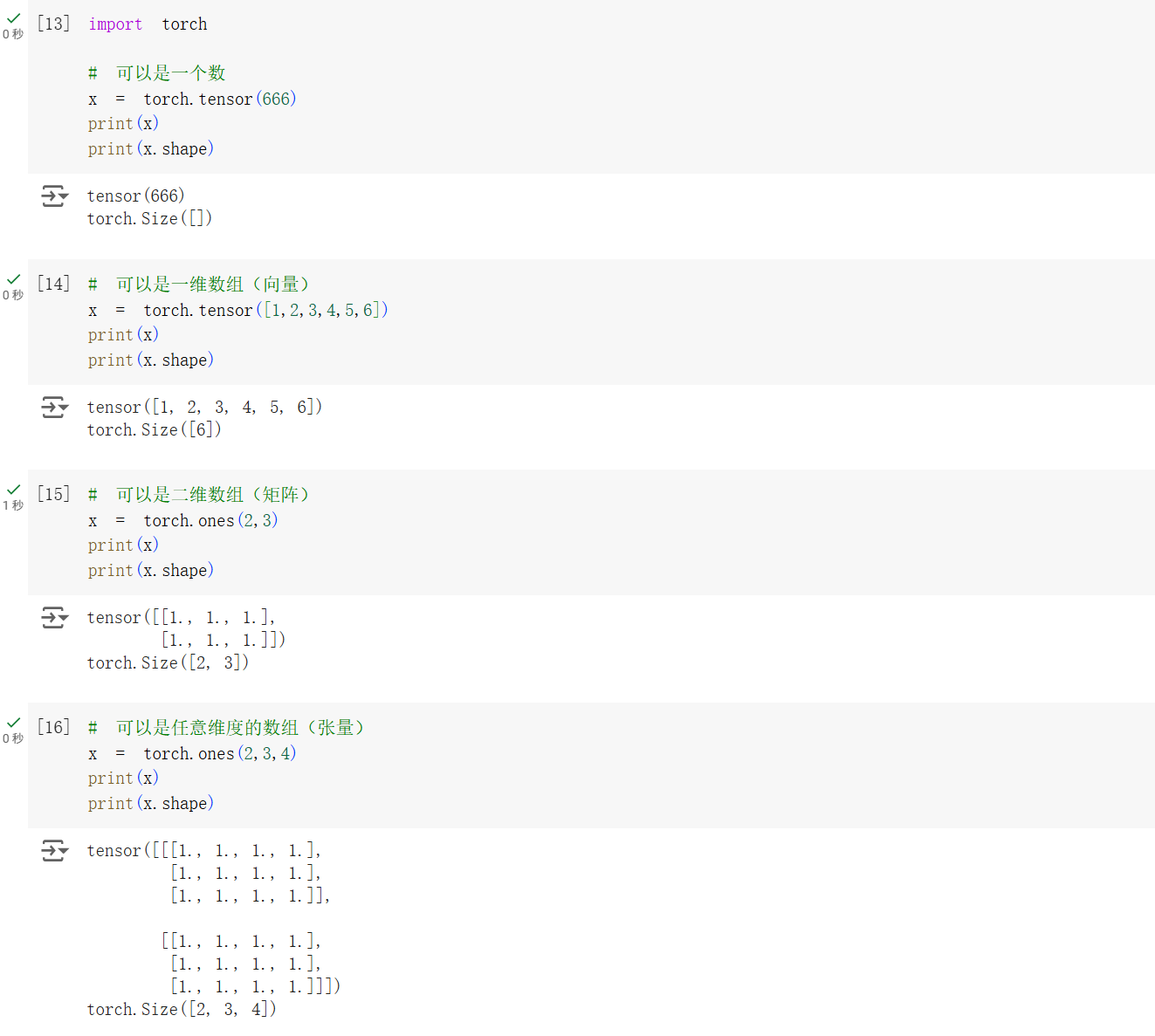
可以看到,对于只有单个数的张量,维度为 0,torch.Size 为空;一维张量的大小即为其数组长度;任意维度的张量的大小即为其各维度的长度。使用 torch.ones() 或者 torch.zeros() 等初始化张量时,输入的就是其张量大小。
对于 tensor 而言,基本上 numpy 有的数据类型它都有并且都做了兼容。可以通过 torch.numpy() 和 torch.from_numpy() 进行互转。
接下来尝试创建 tensor 的各种方法。
| 方法 | 说明 |
|---|---|
torch.ones() | 创建全 1 张量 |
torch.zeros() | 创建全 0 张量 |
torch.eye() | 创建单位矩阵 |
torch.arrange() | 创建等差数列 |
torch.linspace() | 创建等分数列 |
torch.rand() | 创建随机数张量 |
torch.randn() | 创建正态分布随机数张量 |
torch.normal() | 创建正态分布随机数张量,可以指定均值和方差 |
torch.uniform() | 创建均匀分布随机数张量,可以指定最小值和最大值 |
torch.randperm() | 创建随机排列张量 |

可以使用 torch.dtype() 函数打印出张量的数据类型。

可以看到 torch.long 类型在这里就是 torch.int64。
也可以根据已有的张量创建新的张量。
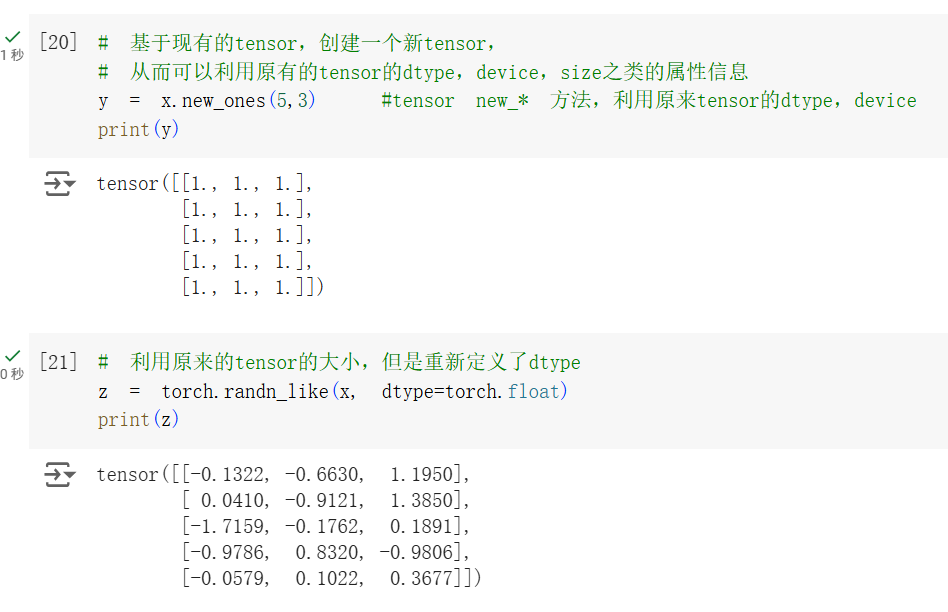
接下来探索张量的各种操作。对于一个张量而言,其其实就是带有维度属性的矩阵,因此矩阵有的基本运算它都有实现。

在这个例子中,使用一个 torch.Size([2, 4]);使用 torch.numel() 打印 m 中元素的数量,即
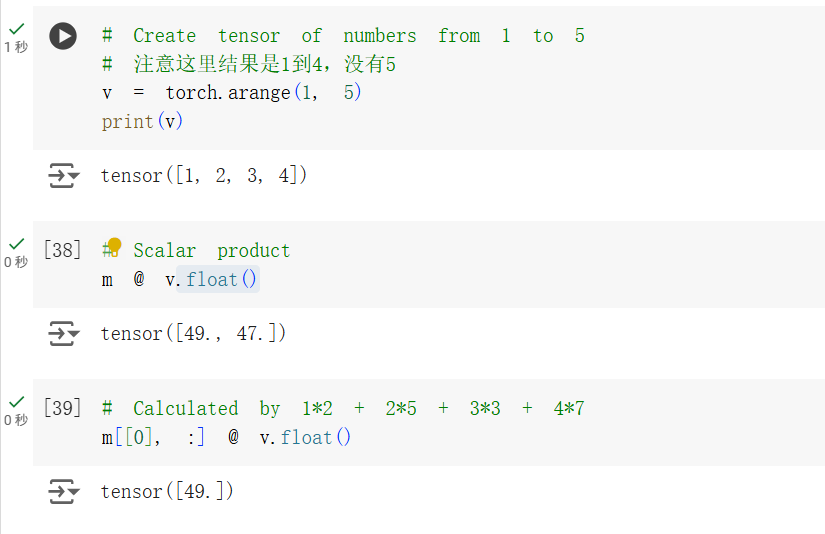
接着使用 torch.arrange() 方法为张量 v 创建一个排列初始化。使用 @ 运算符,即 torch.bmm() 进行矩阵乘计算。这里的注意事项是,m 和 v 的数据类型应当相同才能进行计算,见问题总结与体会部分。
接下来是加法操作、转置和创建等分数列操作。
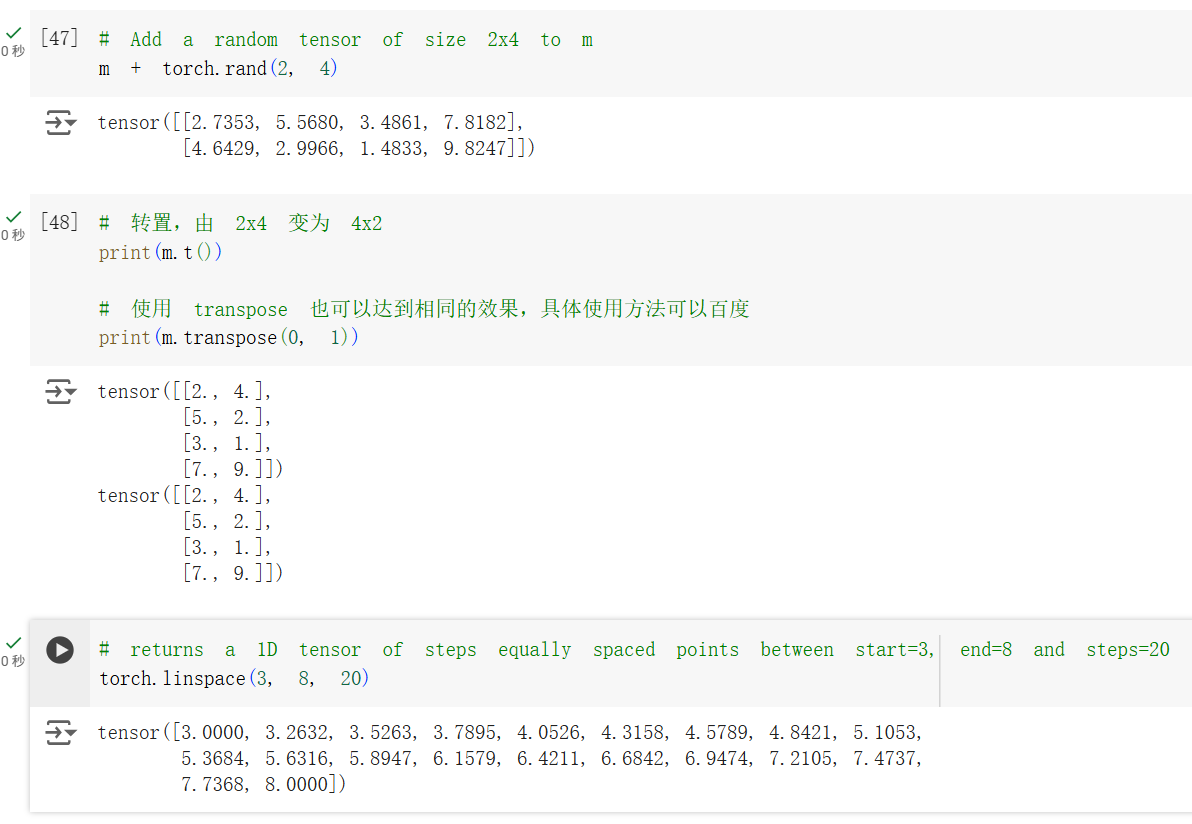
在 torch 中,使用 torch.t() 和 torch.transpose() 都可以实现转置操作。torch.t() 只能对 2 维张量进行转置,而 torch.transpose() 可以对任意维度的张量进行转置,只需要指定转置的维度即可。
前面也有提到,torch 可以很方便和 numpy 进行互转,因此可以很方便使用 matplotlib 进行可视化。
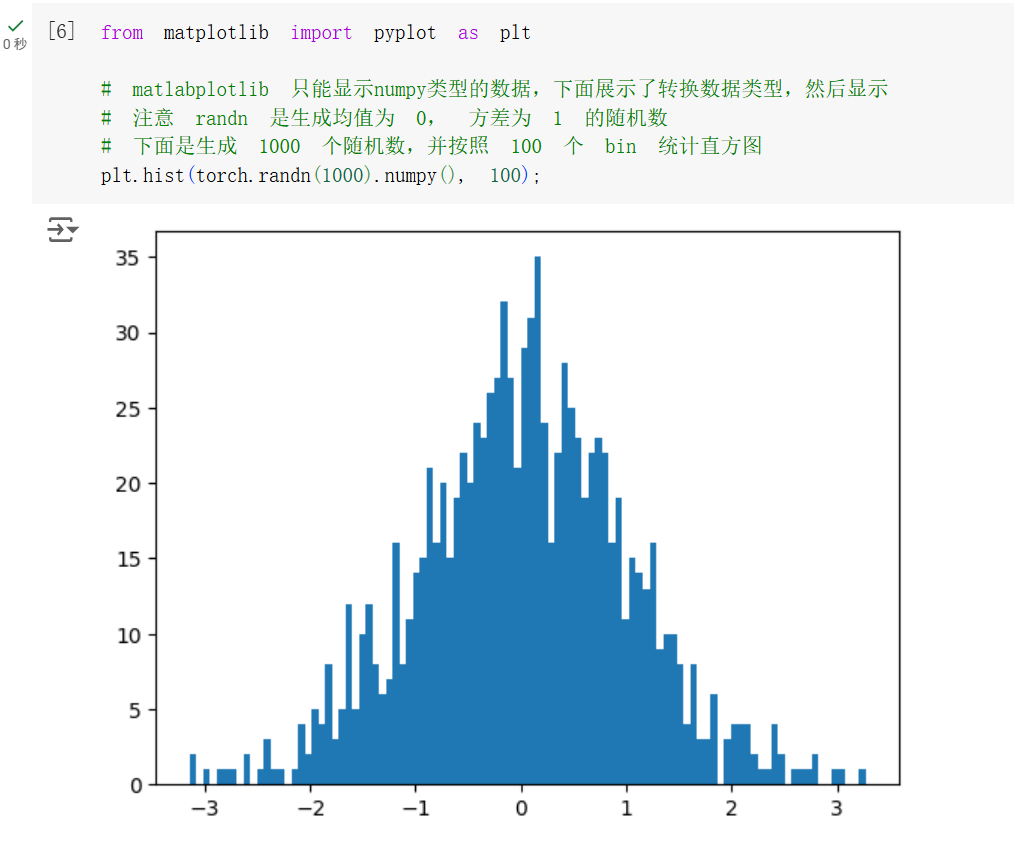
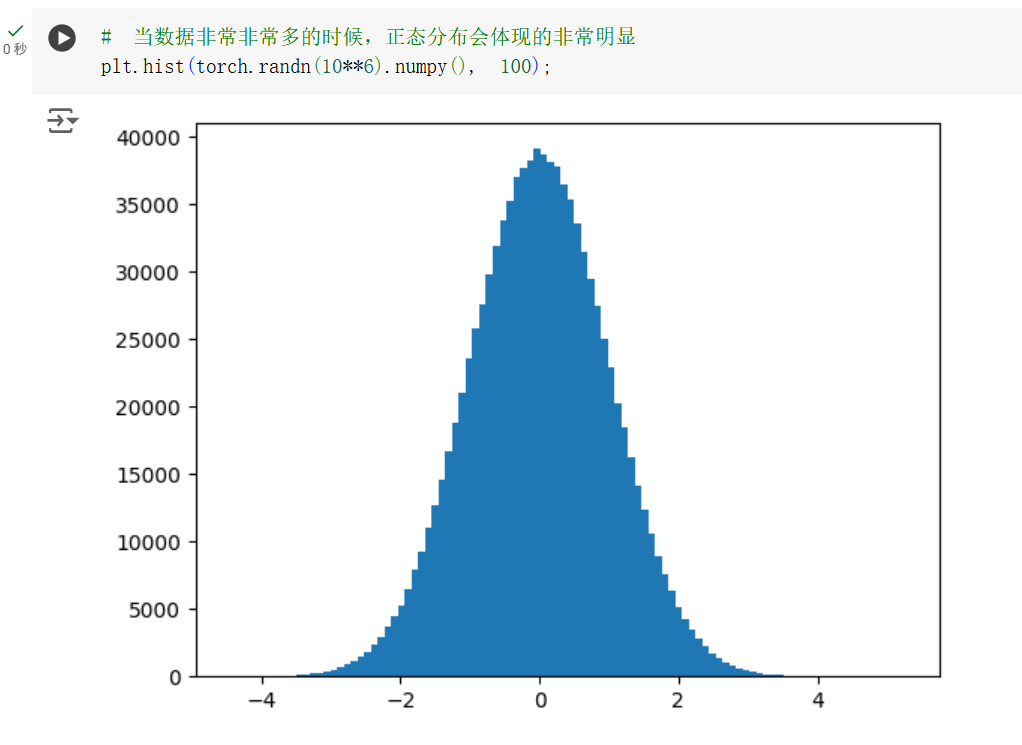
这个例子中可以看到,使用 torch.randn() 生成的随机数十分接近正态分布。
为了实现信息整合,深度学习中常常使用 cat 方法拼接张量。

concatenate 可以从不同方向拼接张量。
螺旋数据分类
使用神经网络进行拟合是很常见的一种应用。螺旋数据分类实验中先下载需要的函数和图像,引入基本的库,初始化。

初始化后输出此时 torch 所在的设备,输出为 cuda 说明成功启用 GPU 加速运算。
接下来调用 torch.zeros() 函数初始化特征矩阵和样本标签。这里的
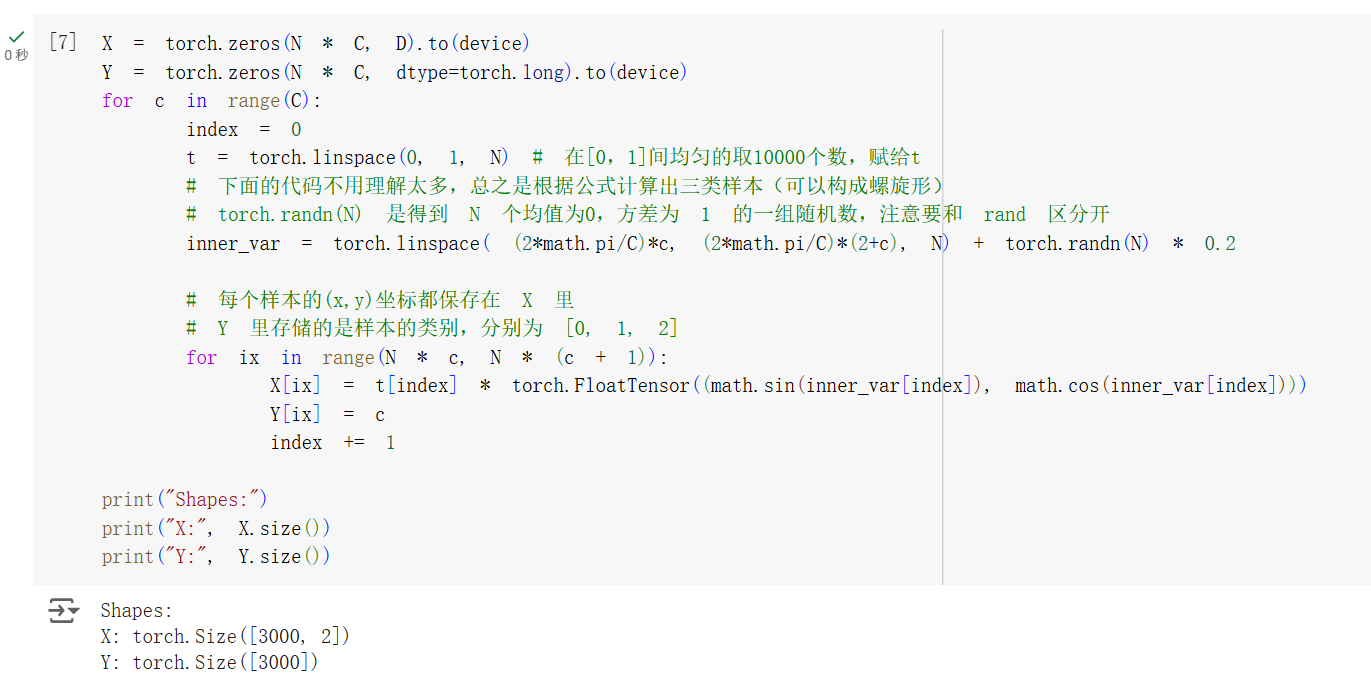
这样初始化后,一共是
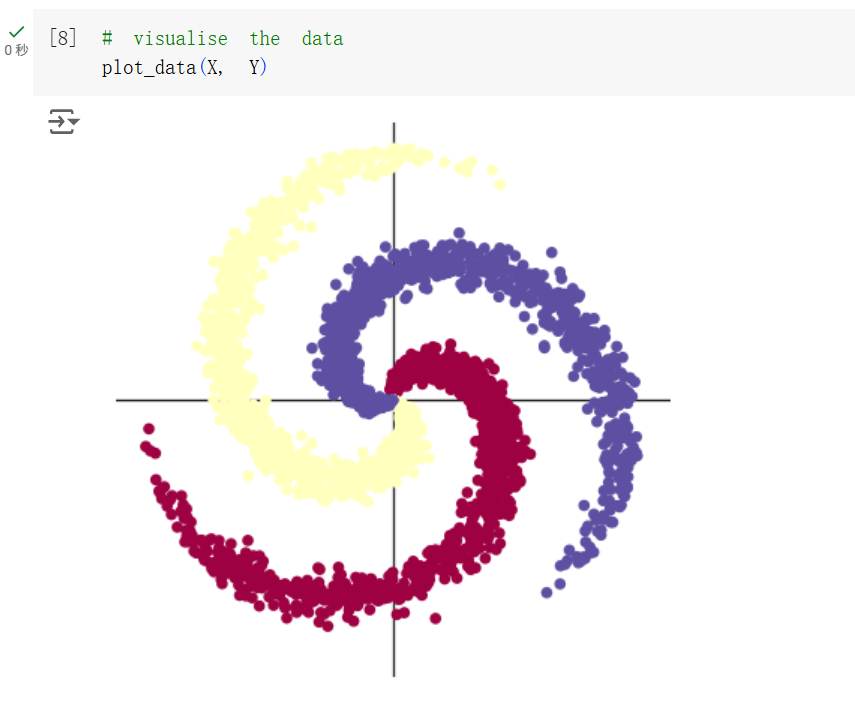
按照实验要求,首先构建一个线性模型:
model = nn.Sequential(
nn.Linear(D, H),
nn.Linear(H, C)
)所谓线性模型,就是通过加权和对特征进行线性变换和平移来训练网络。这个例子中相当于是有两个全连接层组成的线性变换,对于每个样本而言输入的维度是
训练时,由于 PyTorch 为了提高训练效率自动打开了梯度累加,如果不想要之前的 batch 影响到现在的训练批次,则需要对梯度进行清零。
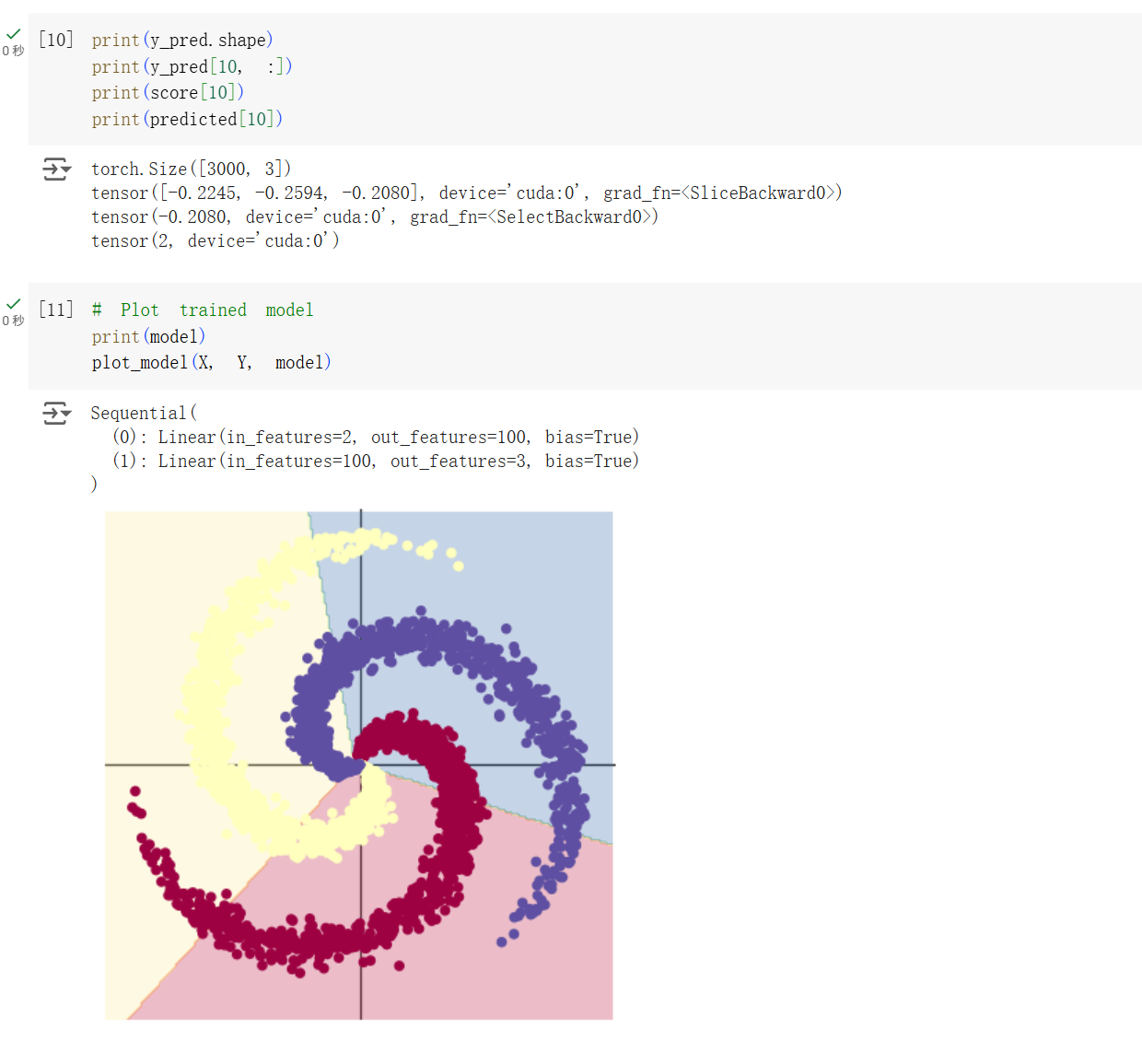
可以看到这样训练出的模型效果并不好,仅仅是三个线性关系(一次函数)划分出的区域。原因就在于,纯一次函数无论如何组合,最后都只会是若干条直线形成的交叉区域,对于这种复杂的图形很难划分。聪明的科学家就想到可以加入一层“激活函数”让神经网络变得不线性,从而改变这个现状。在实验中,就是加入了
通过这种非线性的函数就能很好地优化神经网络学习到非线性的关系,如下图。
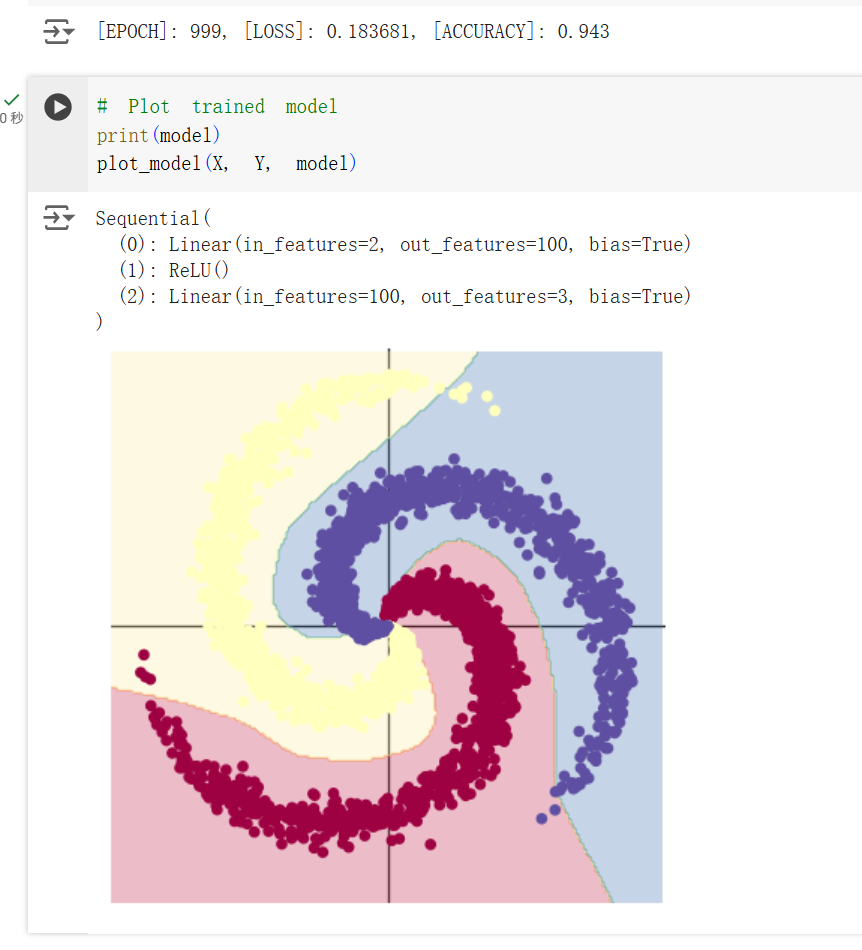
可以看到,经过
二、问题总结与体会
问题 1
在运行以下代码的时候,出现了类型错误的报错。
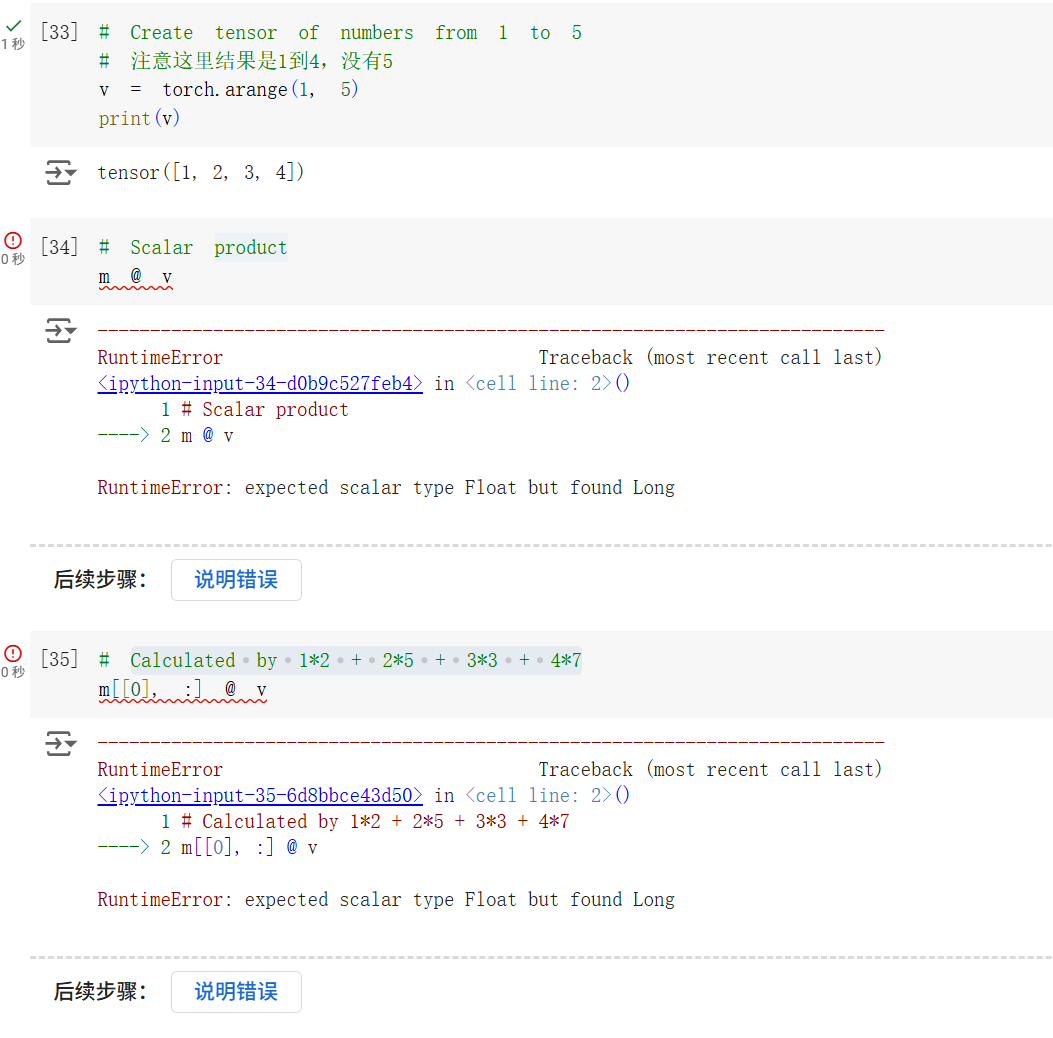
尝试打印 m 和 v 的类型,发现问题,两个运算值的类型不一致,无法进行运算。

添加 .float() 转换类型后,即可正常计算。

@ 运算符对应的是 torch.bmm(),它对应不能作维度扩展的矩阵乘法。在这个例子中,得出的结果就是 [2, 1]。
问题 2
另一个问题倒是小问题,就是路径改了。同时 Colab 需要将一些素材反倒 res 目录下才能正常跑起来。

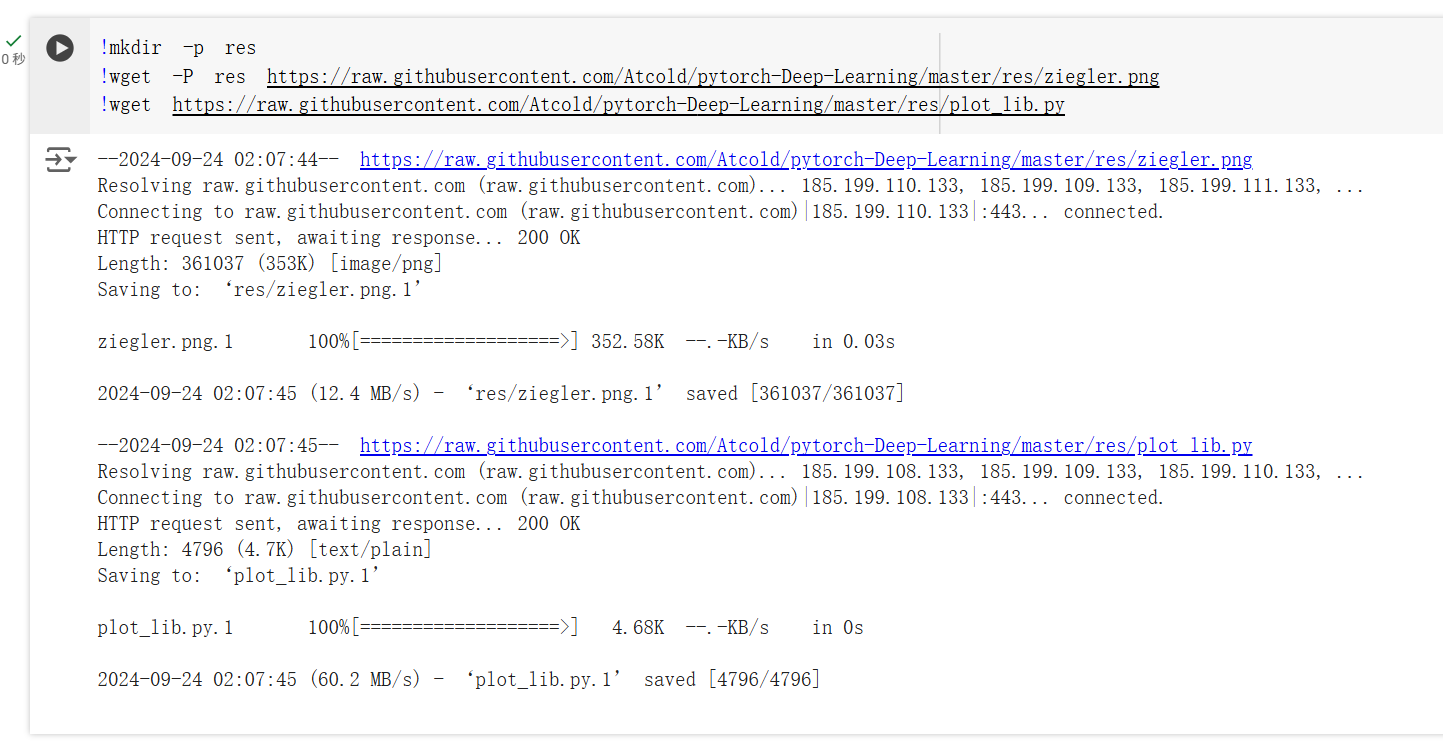
思考题
!!! question "AlexNet 有哪些特点?为什么可以比 LeNet 取得更好的性能?"


和 LeNet 相比,AlexNet 最显著的特点就是变深了。在 LeNet 的基础上它增加到 5 个卷积层、3 个全连接层。由于在两张显卡上进行训练,所以使用两个 pipeline 进行并行计算。和 LeNet 的 $28 \times 28$、$14 \times 14$ 等卷积核相比,AlexNet 使用多层的小卷积核代替之。还有一点不同是 LeNet 使用平均池化,而 AlexNet 使用最大值池化。除此之外,为了加快训练收敛速度,它使用了 ReLU,同时引入 dropout 机制防止模型过拟合。
它能比 LeNet 取得更好的性能,原因可以列为以下几点:
- 深度增加,参数量提升,理所应当模型能够学习到更多的特征;同时更深的网络有利于学到更抽象的特征;
- 训练数据增加,同时使用数据增强的策略将已有数据作变换增强数据训练集;
- 使用 ReLU 而非 LeNet 光滑的激活函数(Sigmoid),大大加快收敛速度,同时避免梯度消失;
- 最大池化能比平均池化产生更好的实验结果;
- 使用了 Dropout 策略防止模型过拟合,保证了泛化性。
!!! question "激活函数有哪些作用?"
- 让神经网络能够学习到特征之间的非线性关系,即将线性的 $wx+b$ 转化为 $\sigma(wx+b)$,让模型能够学习到复杂信息;
- 加快训练收敛速度(ReLU)。
!!! question "梯度消失现象是什么?"
当模型有过深的结构时,如果激活函数导数小于 $1$,链式求导后累乘了许多小于 $1$ 的数,导致梯度越来越接近于 $0$ 以至于权重几乎没有变化,导致网络训练十分缓慢或者无法训练。
!!! question "神经网络是更宽好还是更深好?"
在有足够的宽度保证每层学习特征足够的前提下,更深比较好。
这里假定“更宽”还是“更深”讨论的语境是面对一些复杂任务的时候。更宽和更深本质上都是对应参数量的增加。但增加深度时,相当于再经过了一次卷积、池化操作、激活函数,即又学习到了一次非线性的特征,对于复杂的表达而言这是比增加宽度(线性参数)更有利的。同时每一层的宽度有限,对于每一层而言其可以学习一些简单、递进的特征,越深层学到越高级的特征。

但也不是越深越好,像前面提到的梯度消失正是出现在深度过深的网络中。即使有如上图 ResNet 带来的残差学习能够使深度学习成为可能,但梯度消失、梯度爆炸的问题仍然存在。
!!! question "为什么要使用 Softmax?"
Softmax 将数据视为一个个概率分布,它将向量归一化后使用离散概率分布公式进行计算。这样在分类问题中,就能直接将神经网络的输出转换为各类的概率。有助于加快训练的收敛速度。
!!! question "SGD 和 Adam 哪个更有效?"
SGD 即随机梯度下降,每次随机选取一个样本进行一次参数更新、向梯度反方向移动,缺点恒定学习率导致会震荡、且会收敛到局部极小值;Adam 引入动量的概念,估计一阶和二阶矩(均值、反差),防止梯度震荡,但后期学习率太低。综合来看还是 Adam 更有效一些。但也有人将两个结合在一起用。
总结
经过这次实验又巩固了深度学习的基础知识!希望可以在后面的敏捷开发中添砖加瓦。
